I’ve always wanted an excuse to piddle about with graph theory, so when my multi-agent systems class inspired me to think of a naïve attempt at solving the graph-isomorphism problem, I had to try it.
The inspiration was a network routing algorithm where each node in the network keeps a table of the distances to the other nodes through each of its links. I had to wonder if it would be possible to reconstruct the network simply based on one node’s view of the distances. That doesn’t seem very likely, but if we use that information from all of the nodes, I suspect it may even be trivial.
That’s a slightly different question from the graph isomorphism problem though, because a network is labeled, while an unlabeled graph is not. It does, however, suggest a graph invariant that would solve the graph isomorphism problem provided that any two non-isomorphic graphs produce a different invariant.
The invariant is constructed as a three dimensional array by simply listing, for each vertex, the shortest-path distances to the other vertices through each of its edges. The array is then recursively sorted to normalize it. This gives an invariant with seemingly an awful lot of information (at least in my inexperienced opinion). It didn’t seem probable however, that someone with almost no experience in graph theory had solved one of the biggest open problems in graph theory, so I set out to find a counterexample.
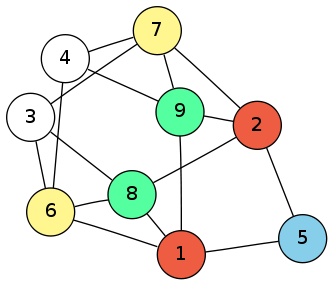
Specifically, I was looking for the smallest pair of non-isomorphic graphs that shared the same invariant. I set one of the computers at my disposal to work on it, and found that the invariant is complete for all graphs with less than nine vertices. For nine-vertex graphs, there are no less than twenty pairs of counterexamples. Here is the pair with the least number of edges:
![HCpdVG] HCpdVG]](/images/blog/58/graph2.png)
The invariant guarantees a few things about these two graphs. They must be the same size and of the same order (same number of edges and vertices), and they must have the same set of edges incident on its vertices: in this case, we can see that both graphs have 6 vertices with 4 edges, 2 vertices with 3 edges, and 1 vertex with 2 edges.
We can tell that the graphs are not isomorphic with a little inspection: if they were isomorphic, then the blue vertices must correspond, since they are the only vertices with two edges. Then the pairs of vertices marked in red must correspond to each other (without knowing which to which), being the two vertices connected to the only vertex with two edges. In both graphs, there are two other vertices that are both connected to the red pair, which are the vertices marked in green. Then there is a third pair of vertices which are connected to one of the red vertices, but not both. These are marked in yellow. Notice that in the first graph, the green and yellow pairs do not share an edge, but in the second graph they do. Therefore, the graphs are not isomorphic.
Showing that they share the same invariant would be a much more laborious task, so I’m going to trust the computer on this one.
This makes me want to start a collection of graph invariants and their corresponding smallest pair of “counterexamples”.
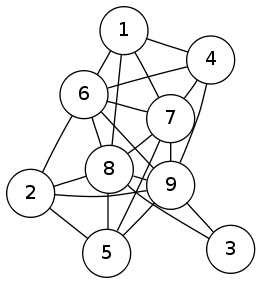
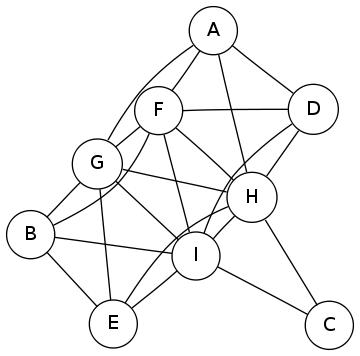
Just because I like pictures of graphs, here’s another one of the twenty pairs I found:
Comments