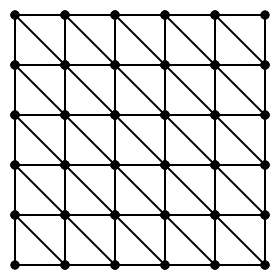
I’ve been spending some of my free time the last week and a half watching Norman Wildberger’s Lectures on Algebraic Topology. One of the things I’ve learned is that an m-by-n rectangle with integer dimensions can be partitioned into 2×m×n triangles with area ½ and corners at integral points. This fact by itself is rather obvious, given the most regular partitioning shown below:
The part that surprised me is that the sides of the triangles can be arbitrarily long, allowing a variety of different shapes, and the whole thing still works out. Here’s another way to partition the 5-by-5 rectangle:
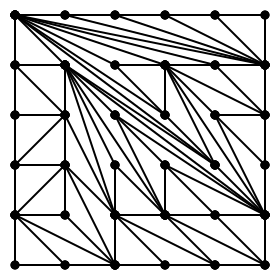
The fact that they all have the same area is a consequence of Pick’s Theorem. I wanted to see what sorts of partitionings you get by starting with a bare rectangle and adding lines at random. And that’s exactly where the image above came from.
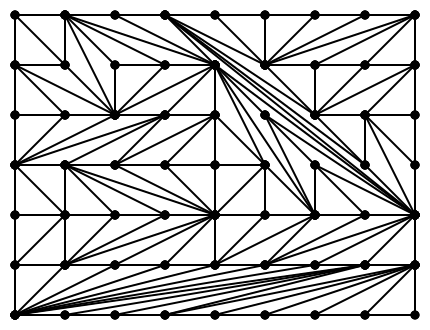
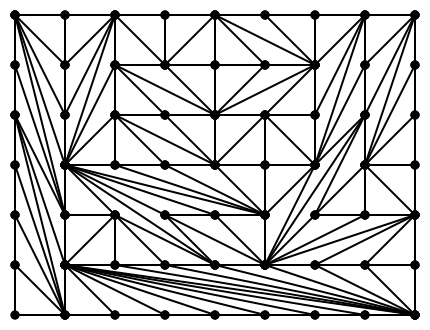
Here are a couple more, just for fun.
Comments