Once again Algebraic Topology compelled me to write code. This time it was the Ham Sandwich Theorem, when I realized that it wouldn’t be too hard to demonstrate the two dimensional version of the theorem with another interactive doohickey.
The interpretation from which the Ham Sandwich Theorem gets its name says that if you have two slices of bread and a slice of ham between them, then no matter what their respective shapes or volumes or how they are positioned relative to each other, it’s always possible to make a single straight slice through the sandwich resulting in all three pieces being exactly bisected.
The Ham Sandwich Theorem applies to any N solids in N-dimensional space, so the 2D version says that any two sets of geometric shapes can be simultaneously bisected by a line. I said “two sets” rather than “two shapes” because the theorem actually doesn’t rely on the shapes even being connected. So we can talk about a collection of red and blue circles, as in the image below:
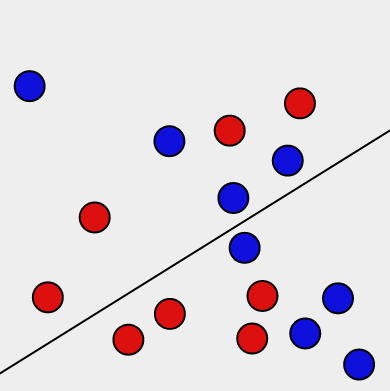
No matter how the circles are arranged, and no matter how many of them there are, there will always be at least one line that bisects both sets by area simultaneously. The interactive version lets you add, remove, and rearrange the circles.
Comments