I've been working on some static visualizations of hash functions, starting with SHA1 and MD5 (images here and here, respectively). The two sample images show the process of computing the respective hash functions on the input "denny" (with ASCII encoding -- i.e., the input in hex is "64656E6E79"). A portion of the MD5 image is included below:
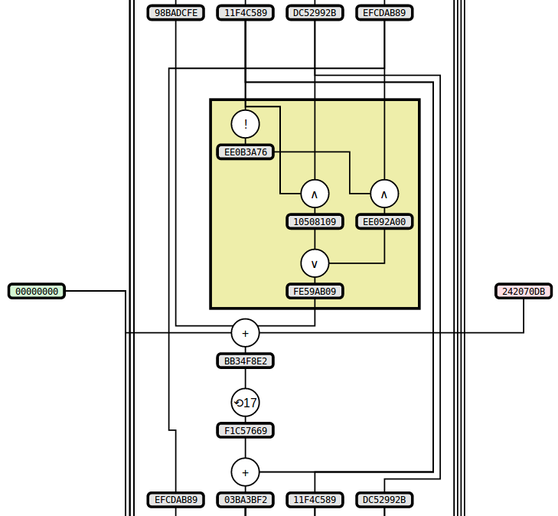
Notes about these two particular algorithms and their visualizations:
- Both algorithms are mostly defined in terms of operations on 32-bit "words", which essentially means 32-bit integers. They define the input/output conversion from sequences of bits/bytes to words, but this step is not covered in the diagrams.
- Probably the most confusing thing if you examine them in detail is that SHA1 uses a big-endian conversion from 4 bytes to 1 word while MD5 uses little-endian. See Appendix A for more. (tl;dr: the words in MD5 have their bytes printed in the opposite order you would expect.)
- MD5 and SHA1 have a lot of similarities, and in particular they both include a function of 3 words that varies slightly throughout the computation; so I've highlighted this function with a yellow box.
- The way that MD5 evolves its state is very similar to SHA1, but it is described differently in the spec. I decided to deviate from the spec and structure the diagram the same way as SHA1, which both highlights the similarity and is also (I think) a bit simpler to follow.
If you're curious about any other details of MD5 or SHA1, the specs are fairly readable, hopefully even more so with the diagrams to follow along with.
I'm hoping this sort of diagram can
- give an appreciation for
- how complex hash functions are, both absolutely and relative to each other
- the difficulty of trying to invert a cryptographic hash function
- be a useful aid to anyone trying to understand the details of a particular algorithm
- be fun to look at. I love things that give a sense for how crazy-complicated computers look from certain angles.
Several things I think are worth exploring:
- How well can this approach be adapted to hairier algorithms?
- Whirlpool uses a 64-byte state rather than a 5-word state (like SHA1)
- A more esoteric algorithm could operate on individual bits
- I'd like to branch out into other sorts of computations
- Other cryptographic primitives
- Numerical algorithms (e.g., big-integer arithmetic implementations)
General feedback and suggestions welcome.
Appendix A
Big-endian looks more natural to me, so I display the hex value for words with the higher-order bytes first -- e.g., the word corresponding to the integer 100 is shown as "00000064". This means that internally both algorithms look the same (in particular the bit-rotations and addition-mod-32 operate the same way), but for MD5 the input and output words will have their bytes ordered the opposite of what you would expect. For the input "denny" where the first word comes from the substring "denn", the first word in SHA1 is "64656E6E" while the first word in MD5 is "6E6E6564". You'll also notice this if you try to compare the MD5 output shown with the value given by any normal MD5 utility.
Comments