Noticing that my Tetris Tiler had been mentioned in a recreational math class at Carnegie Mellon gave me sufficient motivation to dedicate some time during Spring break to pounding out some new features. The most significant is the ability to choose what set of pieces to use, with the set of available pieces being all of the polyominoes of orders two through six. This allows a number of interesting setups that weren’t possible with the fixed set of tetrominos.
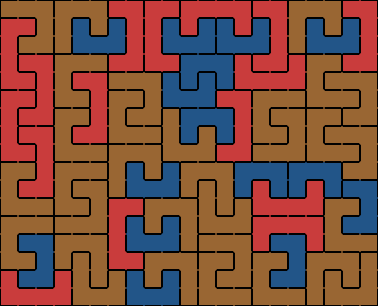
One that I’ve been playing with since I first got the new features functioning is trying to tile an empty grid with a small set of unlikely pieces. Tiling empty grids was never interesting in the older version, because the program always found a boring solution quite quickly and simply. However, with the new features, it’s quite easy to find piece sets that cannot tile a fix-sized rectangular empty grid, and so an interesting problem is finding piece sets for which it’s not at all clear that any such tiling exists. This one is a good example, where each of the pieces are kind of ‘u’ shaped:
This one consists of a bunch of ’t’s:
Another feature I added allows the grid to wrap around vertically or horizontally. This can be used to create seamless repeating patterns, which could be useful, say if you need ideas for tiling your kitchen floor, or a nerdy background for your blog. For a good example, download the image below and set it as your desktop wallpaper, and specify “tiled” (or, if you’re not using Firefox, just click here to see it in a popup window).

It can also be used for this sort of nonsense:
I also added the ability to save grids/tilings, as well as download images (which is where the above images and their links came from). Future features I’m planning on include custom colors, one-sided polyominoes (i.e., distinguishing between mirror images), and an easier-to-use grid editor. You can play with it here.

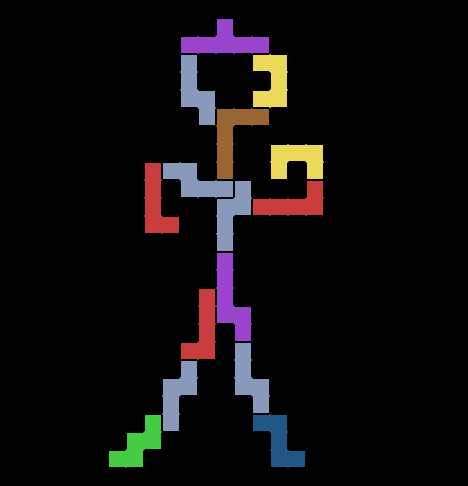
Comments