My recent frolicking about with Graph Theory was facilitated by a database that I populated from these collections, as well as web interface to it with some basic search functions. I just finished polishing the interface to meet my own user-friendliness standards, and have propped it up in the Sandbox here.
It has all of the undirected connected simple graphs with nine vertices or fewer (except the graph with one vertex, which I doubt anyone is interested in), and allows browsing through the database with just about any simple restriction on the attributes of the graph (radius, girth, automorphisms, etc.).
Having the graphs and their attributes pre-computed means that it can be a lot faster to find graphs with particular combinations of characteristics than it would be if everything had to be computed on the fly. It’s also easy to find types of graphs that don’t exist for nine vertices or less, such as asymmetric regular graphs.
As someone with little academic experience with graph theory, I found it a very efficient way to get acquainted with the different types of graph properties and generally increase my familiarity with the subject.
It also tended to prompt deeper questions that aren’t so easy to Google for. For example, I noticed that very few of the graphs had an automorphism-count that was a prime higher than two. Specifically, there are only four of them, all with only three automorphisms, and all on nine vertices. This is one of those:
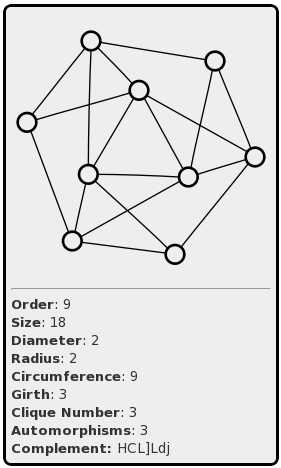
The smallest graph with 2 automorphisms is actually the smallest graph with any edges at all, which is the only connected graph on 2 vertices. So if we form a sequence of the order of the smallest graph with p automorphisms for all primes p, we have the following so far:
2, 9, …
So how does this continue? What is the smallest graph with exactly 5 automorphisms? 7? 11? I can’t find any information on it, but I have to think they might be quite large, such that it would be hard to find them without more sophisticated mathematical analysis. On the hand, they might all be simple variations on the one above.
To avoid the temptation to write a new blog post every time I see an interesting graph, I’ll probably create a list for them. For now, the large-girthed-graphs are fun.
Comments