Lacking the energy to do anything more novel, I was pooting about on the old small graphs app, and noticed for the first time that I could use it to search for graphs with any two given degrees. So I tried one and three:
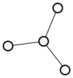
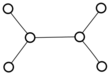
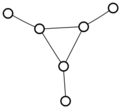
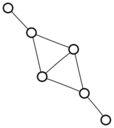
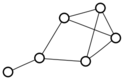
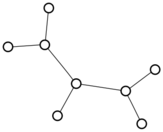
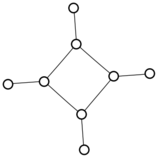
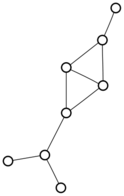
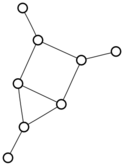
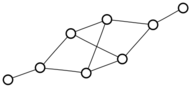
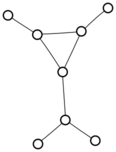
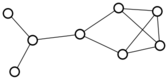
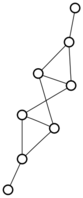
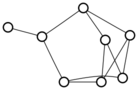
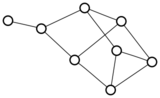
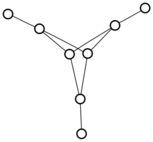
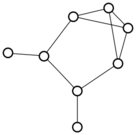
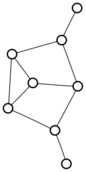
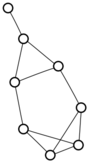
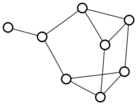
There were only twenty results, so I was able to look through all of them pretty quickly. The first thing I noticed was that the largest ones had only eight vertices, even though the app also searches graphs with nine. That meant that of all the 261080 connected graphs with order nine, none of them had just degrees one and three.
I checked the orders of the other graphs in the set of twenty: there were four that had six vertices, and one that had four. That meant that every example of a graph with degrees one and three had an even number of vertices. Hmmm.
So is that always true? One trivial property of graphs is that the sum of all of the degrees must be even — this is because when you sum the degrees of the vertices, you necessarily count every edge exactly twice. So we’re looking at graphs where all of the degrees are one and three, and we know they have to sum to an even number.
But if you want a set of odd numbers to sum to an even number, you have to have an even number of odd numbers in the set — two odds always sum to an even, so if you have an even number of odd numbers, you can pair them up and get half as many even numbers. But if you have an odd number of odd numbers, one will be left out, and the total sum will have to be odd.
So yadda yum bladdy blah and every graph with degrees one and three must have an even number of vertices. One of my favorite kinds of proofs are the kind that prove something is impossible, despite the fact that you can imagine a whole host of possible scenarios where it might be true. There’s certainly an infinite number of this kind of graph, but no matter which one you choose (or whatever even-ordered graph of any kind that you choose), there is never a way to add just one vertex such that the new graph has only degrees one and three.
Comments