One bit of algebra that particularly fascinated me in high school is the theorem that for any set of N points in the cartesian plane with distinct x values, there is a polynomial curve with degree at most (N-1) that passes through each of them. For a set of points, you can find the relevant polynomial using a system of N equations with N variables.
A quick corollary is that for any finite sequence of N integers, there is a polynomial function which for input (1,2,…,N) produces that sequence.
A friend of mine is teaching high school math and seems to be on a somewhat related topic, so I made a little interactive doo-hicky that takes an input sequence and computes the polynomial function.
One thing I didn’t anticipate is that it looks like the resulting functions always map integers to integers. This certainly doesn’t seem obvious to me, and I don’t know how I would go about proving such a thing. I’m sure that if it’s true, it’s already been proven, likely hundreds of years ago. But it’s strange that I’ve never heard of it.
Labeled Balls in Indistinguishable Boxes
2010-10-10This morning I thought of a nice little combinatorial pattern, and so I investigated a bit.
Consider the set of finite nonempty sequences of positive integers starting with 1, with the restriction that a number N cannot appear in the sequence until N-1 has appeared. For any given length, the subset of sequences of that length is finite, so we can list them. For length 1 we have just the sequence containing the number 1. For length 2 we have (1 1) and (1 2). For lengths 3 and 4 there are 5 and 15 sequences respectively:
1,1,1 1,1,2 1,2,1 1,2,2 1,2,3 1,1,1,1 1,1,1,2 1,1,2,1 1,1,2,2 1,1,2,3 1,2,1,1 1,2,1,2 1,2,1,3 1,2,2,1 1,2,2,2 1,2,2,3 1,2,3,1 1,2,3,2 1,2,3,3 1,2,3,4
If we plug the sequence (1 2 5 15) into the Encyclopedia of Integer Sequences, we find the Bell numbers, which I had not heard of until now. They have a Wikipedia article as well.
Apparently the Bell numbers have a number of interpretations (though with a brief scan of the OIES entry I didn’t see mine), and the easiest one to relate to these sequences is the “number of ways of placing n labeled balls into n indistinguishable boxes”.
To see the connection, say we have n labeled balls. A particular placement into indistinguishable boxes will correspond to one of these sequences. Assume our balls are labeled from 1 to n. Then we’re going to create a list of the boxes that each ball goes in, in order of their labels. Since the boxes are unlabeled, we can give them names: call the box that the first ball goes into “1”. Then call the next new box in the list “2”, and the next new one “3”, and so on. In this way we’ll get a sequence of n positive integers, not necessarily ever greater that 1 (perhaps all the balls went in the same box), but with the property that any number N does not appear until N-1 has already appeared.
Here are the 52 sequences of length 5:
1,1,1,1,1 1,1,2,3,3 1,2,2,1,2 1,2,3,2,1 1,1,1,1,2 1,1,2,3,4 1,2,2,1,3 1,2,3,2,2 1,1,1,2,1 1,2,1,1,1 1,2,2,2,1 1,2,3,2,3 1,1,1,2,2 1,2,1,1,2 1,2,2,2,2 1,2,3,2,4 1,1,1,2,3 1,2,1,1,3 1,2,2,2,3 1,2,3,3,1 1,1,2,1,1 1,2,1,2,1 1,2,2,3,1 1,2,3,3,2 1,1,2,1,2 1,2,1,2,2 1,2,2,3,2 1,2,3,3,3 1,1,2,1,3 1,2,1,2,3 1,2,2,3,3 1,2,3,3,4 1,1,2,2,1 1,2,1,3,1 1,2,2,3,4 1,2,3,4,1 1,1,2,2,2 1,2,1,3,2 1,2,3,1,1 1,2,3,4,2 1,1,2,2,3 1,2,1,3,3 1,2,3,1,2 1,2,3,4,3 1,1,2,3,1 1,2,1,3,4 1,2,3,1,3 1,2,3,4,4 1,1,2,3,2 1,2,2,1,1 1,2,3,1,4 1,2,3,4,5
Comments
Walpha
2010-10-07I asked Wolfram Alpha to do some unit conversion arithmetic for me, and it gave me all kinds of related information, but forgot to give me what I had asked for:
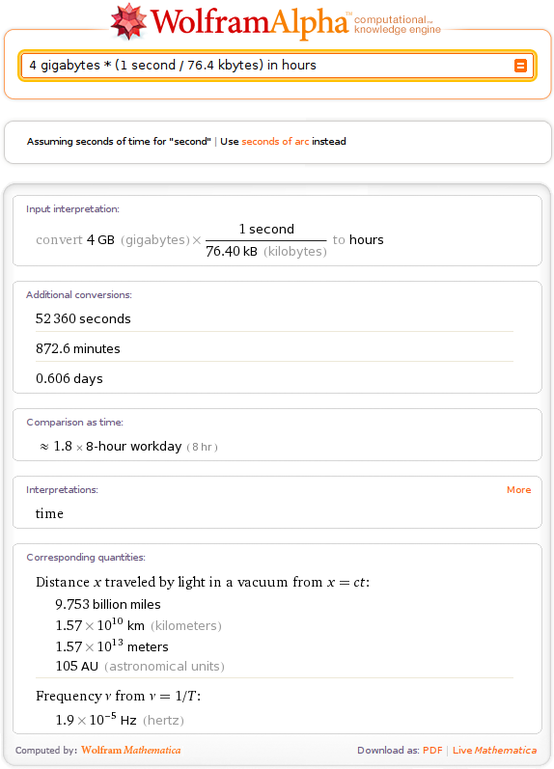
Comments
Graph Graphs
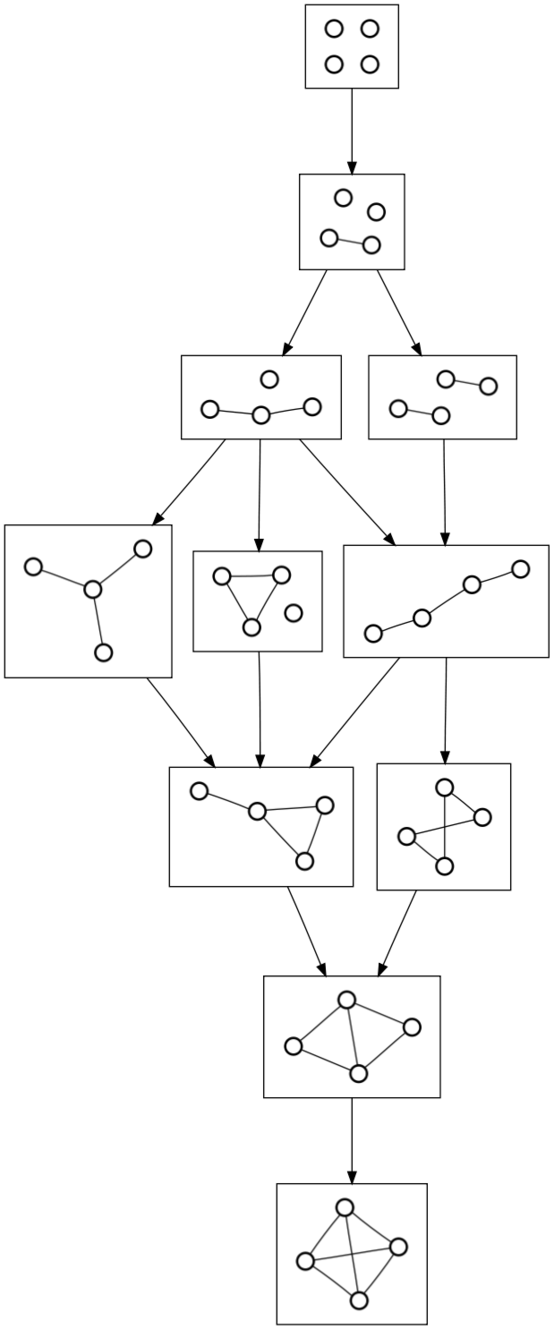
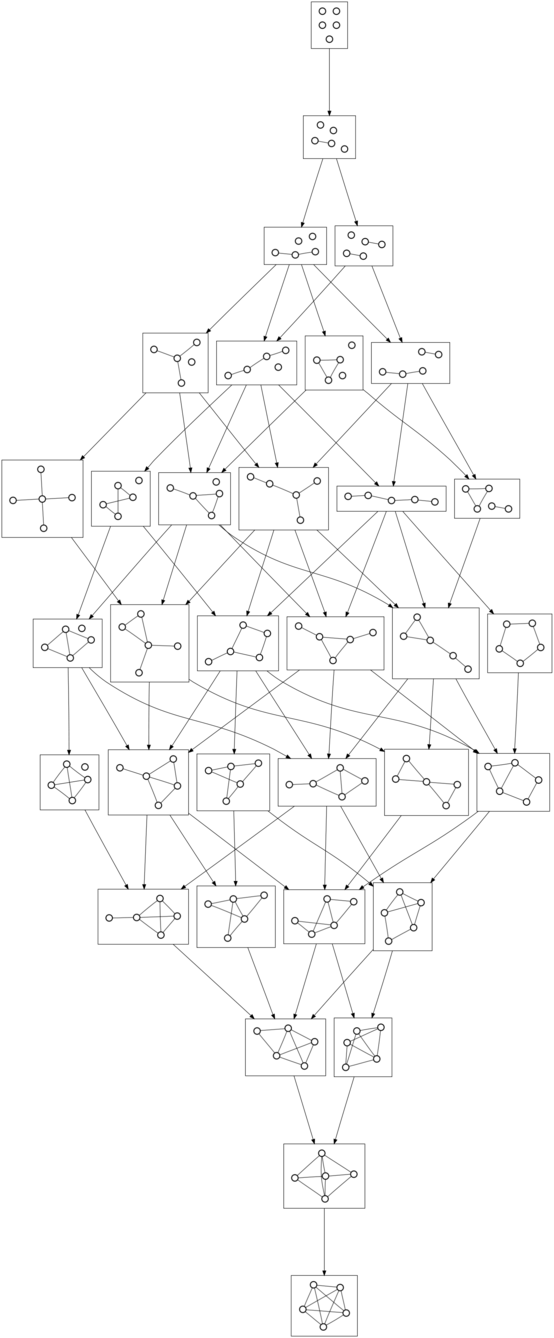
2010-10-06Just because I wondered what it looked like, I generated a few directed graphs of undirected graphs:
The vertices in this directed graph are all of the undirected graphs on four vertices, where two graphs are connected if you can add an edge to one to obtain the other. Here’s five and six:
Comments
Visualizing Tic-tac-toe
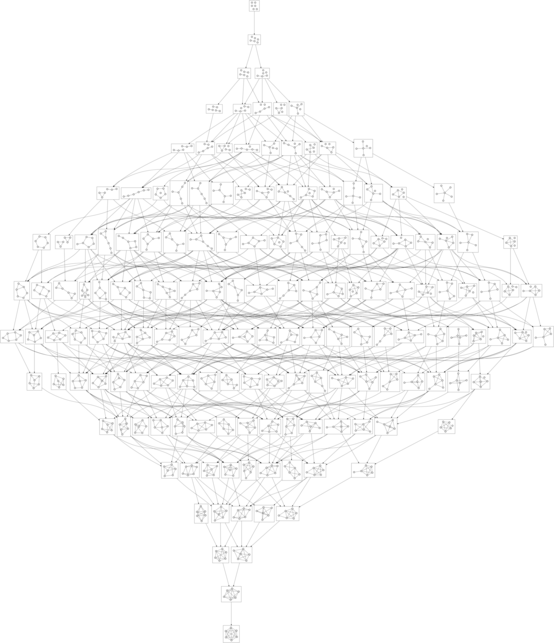
2010-09-18Just a few days ago a lucky train of thought arrived at the delightful realization that the game of Tic-tac-toe is just barely small enough to be graphed out in its entirety. Despite the fact that there are 19,683 different arrangements of X’s, O’s, and blanks on a 3×3 board, and 362,880 different orderings for the nine squares, if we eliminate symmetry and recognize when different sequences of moves lead to the same position, there are only 765 distinct board positions reachable through normal play. All we have to do is hook them up:
In that image and the others (which you should click on to see them at a reasonable size), positions are colored green when they are winning for the first player (X), red when they are winning for the second player (O), and yellow when they are tied. The transitions between positions are solid for good moves and dashed for bad moves.
The graph of the complete game of Tic-tac-toe is a bit much to take in all at once, but there are some interesting subgraphs as well. For example, this is the graph of all perfect games (where neither player makes a mistake):
It doesn’t go without saying that all of the positions in that graph are tied (so I omitted the coloring).
On the other hand, this is the graph of all games where almost every move is a mistake (all but the first and the last, which can never be):
One of the more interesting things I noticed when playing with these data structures is that there are certain positions which are tied, but cannot be reached without making mistakes. For example here are graphs showing two tied positions that can only be reached by the first or second player making a mistake, respectively:

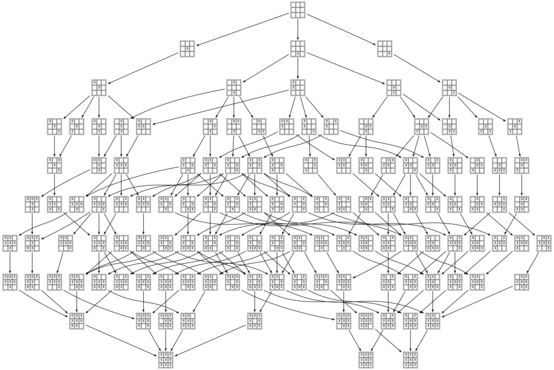

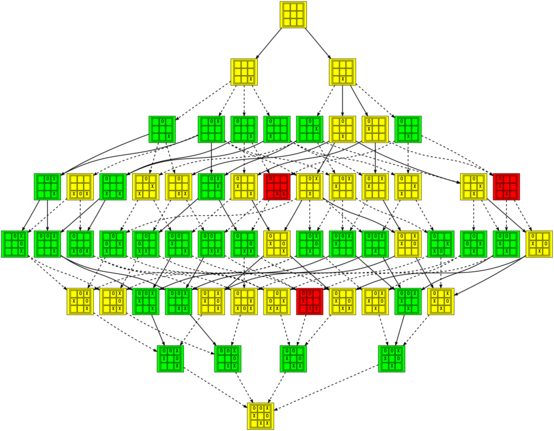
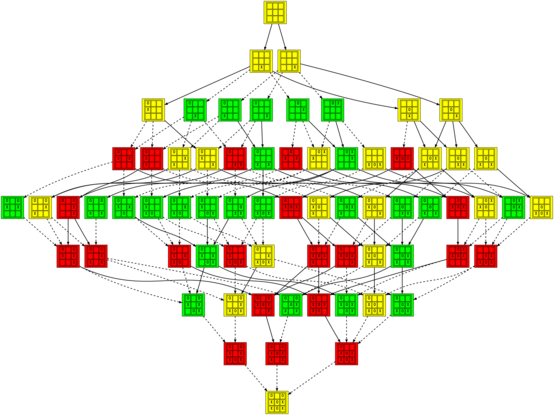
Comments