It occurred to me yesterday that transactions can help database performance in certain cases. Specifically when multiple UPDATE’s, INSERT’s, and/or DELETE’s are used sequentially.
The reasoning goes like this: the most expensive part of any database update is flushing the changes to disk. If you have several successive updates(/inserts/deletes), then the default behavior in most databases is that they will be flushed to disk one at a time, sequentially, forcing you to wait a full round trip for every change you’re making.
Contrast that with a transaction which is guaranteed to be atomic: if the whole group of changes is written to disk altogether or not at all, that means the database is free to hold everything in memory until it’s committed, and perform the commit with a single flush to disk.
Just to make sure I wasn’t crazy, I pulled out ActiveRecord and ran a couple tests (source code here). The results: I wasn’t crazy. For two successive inserts, the transaction version ran in half the time. For twenty successive inserts, the transaction version ran in just over a tenth of the time.
JavaScript Missing Semicolon
2010-09-13For maybe the first time ever, I produced a bug in my JavaScript code that was the result of a parsing ambiguity created by omitting the semicolon at the end of a statement:
console.log("blargh")
(function(){
alert("ah ha ha ha");
}).defer();
And so Ye Olde Firebug complained that console.log(“blargh”) was not actually a function. The misunderstanding stemmed from the fact that the first character on the second line is an opening parenthesis, which apparently causes the parser to assume the return value of the previous expression is a function that I intend to call, even though it’s on a separate line.
The lesson here, kids, is that you should always include the semicolons in your JavaScript. If you don’t, you might end up like me: having to waste an average of ten minutes every eight years or so picking parsing mistakes out of my sloppy, lazy code. DON’T LET THIS BE YOU!
Comments
SHA Collisions
2010-09-11I once saw a talk on git where the presenter casually mentioned that the probability of a SHA-1 collision is less than that of being struck by lightning. This certainly sounds plausible for two arbitrary values (where the probability should be one in 2160), but in a situation like a git repository with thousands of objects each identified by its own hash, I have to wonder how significant the effects of the birthday paradox are. So I pulled out the old Ruby interpreter to find out.
I decided to go with the assumption that a good sized git repository has 100,000 objects it it. I have one at work with over 50,000, so this seems reasonable. Given 100,000 objects, and the assumption that all hashes are equally likely, the probability of a collision is one in 2923295604222228059227973022624136543197. That’s less likely than flipping a coin 131 times and seeing all heads. I’m not worried about SHA collisions anymore.
Comments
Graph Encodings
2010-09-05I enjoy thinking about encoding problems, where an object in one domain needs to be converted to another domain in such a way that the original object can easily be retrieved.
In most applications the encoding domain is strings, and the problem of coming up with the encoding is rarely difficult, as long as you’re careful. Usually a markup language like XML or JSON makes it particularly easy.
I’ve been wondering about less straightforward encodings, which started when I thought of the problem of encoding a directed graph in an undirected graph. Clearly the opposite problem is easy: to encode an undirected graph in a directed graph, simply choose a direction for each edge (this is apparently referred to as orienting the graph). Then the original undirected graph can be obtained by discarding the directions of the edges.
But directed graphs clearly contain more information than undirected graphs with the same number of vertices and edges, so any encoding method will have to generally increase the order of the graph. The best tactic I can think of is to encode the directed edges as vertices in the undirected graph. For example, consider the simplest non-trivial directed graph:

Obviously, we can’t encode this as an undirected graph with just two vertices — we wouldn’t know if there was just one directed edge being represented or two. And if the graph was larger and the two vertices were distinguishable, we wouldn’t know which vertex was the head and which was the tail. So we definitely need another vertex to represent the edge. One vertex doesn’t improve the situation, however, as we still only have one option:
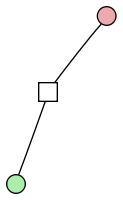
So it looks like we need at least two extra vertices to fully represent each edge with its direction. As best I can tell, the simplest way to do it is like this:
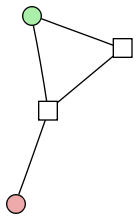
We connect the two edge-vertices to each other, so we know they’re related. Then we connect one of them to the tail, and both of them to the head, so we can tell which is which. Here’s how it looks for a more complex graph:


There is an issue, however, with going in the opposite direction: how do we distinguish the edge vertices from the vertex vertices? The colors and shapes in the previous image make it pretty easy, but they’re not actually part of the graph. The undecorated graph looks like this:
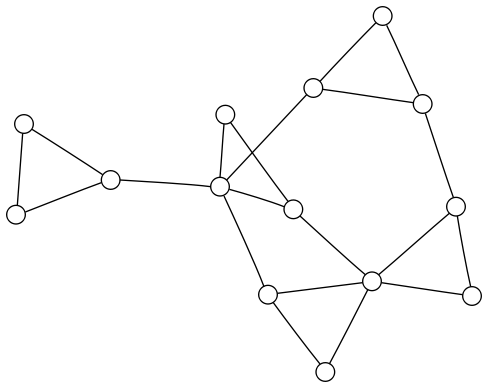
It’s not so obvious how to get back to the original directed graph, or if a general method exists at all. The simplest way I’ve thought of to address this issue is to tack an additional vertex on to each vertex-vertex. Rather than explain that more clearly, I’ll illustrate it. Our first graph will look like this:

Essentially each vertex from the directed graph is being represented with two vertices, only one of which is connected to anything else. Since these second vertices will be the only vertices in the graph with degree one, they’re easy to identify. Here’s the larger graph:
Just for kicks, here’s another pair of graphs where the directed graph was randomly generated:


One question I haven’t settled is whether the extra vertices are strictly necessary. More formally, if we encode without them, are there any two digraphs that encode to the same graph? If I figure anything out, I’ll post it.
Comments
Clojure Farm
2010-08-20Every so often I come across a computational problem (usually of a more academic/theoretic flavor) that would benefit from some combination of the following features:
- Distributed computation with:
- a flexible setup where nodes can be added and removed easily
- no need for any special network configuration, allowing participation from any arbitrary internet-connected computers
- The state of the computation can be easily saved, and is persistent across reboots and power failures
- The state of the computation can be easily backed up and restored in the case of severe failure
- New instances of the computation (and entirely unrelated computations) can be added and run in parallel on the same set of nodes without any extra effort
I’m referring mainly to a special class of problems, where most of the computation consists of pure functions that have small inputs, small outputs, but can run for a long time (long enough to justify the overhead of computing the function on a remote node). They are problems that can never have too many CPUs working on them.
Generally when these kinds of problems come up they aren’t important or interesting enough to bother building such a framework, and so it just doesn’t get done. I have a couple times shambled together an implementation in Erlang, which famously supports distributed computation natively using message passing. However, this really only provided support for features 1a and 4. Also, as fun as Erlang is in a sort of exotic way, the syntax and libraries can become tedious when you try to work on more abstract problems.
I’ve been wanting a good framework for these kind of problems for long enough that I put in a good amount of time designing and prototyping during the summer. I decided that the simplest way to handle the distributed aspect was to use a client-server model with standard HTTP. The only network requirement is one permanent server that can listen for HTTP requests from anywhere on the Internet, and such a thing is certainly not hard to come by (most people can probably do it from home). The server will keep the current state of the computation persisted in an ACID-compliant database, which makes it resistant to all but physical damage to the server itself. That risk, of course, is mitigated with diligent backups.
As for a general method for moving computation around, I think the simplest idea is for the server to send actual source code for the clients to execute. This choice has a strong impact on what language the problems should be written in, and suggests a homoiconic language where the source code can be easily manipulated by the program. Once we’ve used the word “homoiconic” in a sentence, it would be completely inappropriate if the following sentence didn’t proceed directly to Lisp. So I decided to go with Clojure, which is the new Lisp-For-People-Who-Write-Real-Programs. With Clojure we get a highly dynamic language to work with, and the only requirement on the client side is that the JVM be installed.
After deciding on the architecture, there was still challenging design work left to be done, particularly regarding the issue of how to write code for such a framework. I started with the concept of a task, which is just a piece of code to be executed on a remote machine, ideally running for several minutes, and with the result to be returned to the server. At first I decided this was sufficient, and that separate programs would have to be written to interface with the server or the database directly to set up the tasks, process the results, etc. Then I realized there would be value in being able to run long-running computations within the framework and not need any third party program to tie things together.
So the first requirement that comes to mind is that a task should be able to create other tasks. We don’t want a single task to run for more than a few minutes so that we minimize the time lost when a node goes down. So tasks being able to spawn new tasks is definitely required.
Obviously then the new tasks should have access to whatever it is that the old task computed, so they can pick up where it left off. And this suggests some sort of blocking mechanism, where you can create a task that is dependent on the value another task (or set of tasks) is computing. A simple example of this is a map-reduce algorithm, where the reduce task will have to wait until all of the map tasks are done. This seems natural and useful, but if the only concept we have is that of tasks, things get messy when the map tasks are long-running and need to spawn more tasks themselves. How does the reduce task know that the computation it’s waiting on is actually complete?
So I could tell that I needed some better-developed constructs. The best strategy I thought of for solving this problem is to separate the concept of returning a value from the concept of a task. For this I borrowed the term “Promise” from Clojure (which I’m considering returning if I can just come up with a good enough term of my own).
A promise is a placeholder for a value to be computed, as well as a reference to the value after it has been computed. A task has access to the promises given to it by its parent, and a task can create new promises as part of its return-actions. Any task with a reference to an undelivered promise can choose to deliver that promise, but a promise can only be delivered once. If several tasks are trying to find a value to fill the same promise, they can be registered to be canceled if the promise is delivered by another task first.
Tasks can also have promises as prerequisites — a task will not execute until all of its prerequisite promises have been delivered. In the case of a map-reduce algorithm, the map tasks will all have promises to deliver when their final value is computed, and the reduce task will have all of those promises as prerequisites. Note that the problem mentioned earlier of the map tasks not being able to spawn child tasks has been solved, because now any map task needing to spawn child tasks simply passes along the promise to whoever needs it.
So promises serve to tie tasks together. The rest of the entities are fairly straightforward, so I’ll cover them quickly. An assignment is a collection of tasks. More specifically it is one initial tasks and every task that is created from the initial task. It is a thing that you want to do. The tasks and the promises tying them together all fall under one assignment. The goal of the assignment, the final thing(s) to be computed, are implemented as “results”. A result is any final product of the assignment, not to be used again within the assignment, but to be consumed or processed by whoever created the assignment in the first place. Any task can create a result at any time, and an assignment can contain as many results as the tasks produce. An assignment can run infinitely, always producing more and more results.
A project is a collection of assignments that share common libraries. The libraries are where the real code should go — the code that makes up the tasks can be trivial, just a function call with some basic arguments.
I’ve been thinking about these ideas for a few weeks now, and I’ve convinced myself that they’re sufficiently general to be of use for a lot of problems. There may be certain kinds of problems that cannot be easily implemented using these constructs, but I hope that there will be lots of problems for which it will be useful.
I have a prototype with the following features already implemented:
- It works! There are several tests that I run regularly with fifteen to twenty clients connected and a multithreaded server in front of the database. The most nontrivial of the tests computes a Fibonacci number using naive recursion.
- Any internet-connected computer with a JRE can start participating in the computation with a one-line command. It’s that easy in Linux (and I assume Mac) at least. In Windows it shouldn’t be much harder, if at all.
- Worker nodes run the code on multiple threads, taking full advantage of multi-core chips.
- The server takes full advantage of the ACID properties of the database, so that the computation is persisted to disk at every opportunity, and is always in a consistent state. It expects the worker nodes to fail and takes appropriate steps to recover. If the server fails, the workers will wait for it to be brought back up and everything continues where it left off. Backup can be done as a routine database backup.
- A web interface allows the user to see what clients are connected, browse the various projects and assignments to see statistics, create new projects and assignments, etc.
- A debugging mode tracks the significant events within an assignment’s lifetime, and creates diagrams of the computation using Graphviz.
And more features that are close to being implemented:
- Code libraries (which are associated with projects)
can be edited in the web application, while
assignments are currently using them, and versions are tracked
automatically.
- Older versions of code are kept as long as there are assignments using them.
- Assignments using old versions of code can be upgraded to newer versions while they’re running (though you would have to be especially careful with this feature).
- The user can request email alerts when results from a particular assignment are posted.
- Assignments can be created and results consumed programmatically via a restful interface.
- Flexible controls allow the user to assign priorities to projects and assignments.
- Tasks can dynamically determine how many subtasks to branch into based on how many tasks are currently running in the assignment.
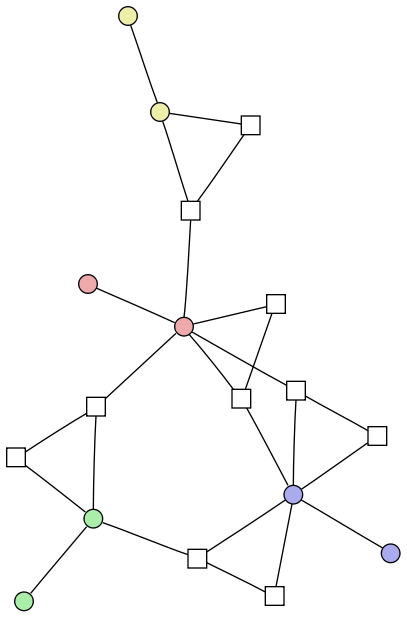
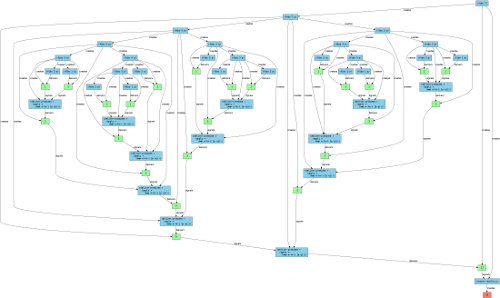
I mentioned the Fibonacci implementation as well as the debugging tool that creates diagrams, so I’ll demonstrate both of those here. The naive recursive Fibonacci function (with the source code here) takes the definition that f(n) = f(n-1) + f(n-2) and computes both recursive calls separately. In this case every call to the function results in five objects being created: two tasks for each recursive call with two promises to store the results, and a third task that waits for the promises to be delivered and adds them together.
Without getting too detailed, if we use this implementation to compute f(7) (where f(1) = f(2) = 1), the debugger produces the diagram below. In this diagram the blue elements are tasks, the green elements are promises, and the red element is a result. You can click on the image to see a larger readable version, or download the svg here.
With most programming projects, making it usable for yourself is a lot easier than making it usable for others, and this is no exception. I am almost to the point where I will start using this for my own projects, but it’s not yet good enough that I would recommend it to anyone else. So I’m curious if anyone thinks they could make use of this, or would like to help with it. I definitely don’t see this as being any kind of commercial product, but just something to help individuals and groups better harness computer power to work on certain kinds of problems.
Comments