Lacking the energy to do anything more novel, I was pooting about on the old small graphs app, and noticed for the first time that I could use it to search for graphs with any two given degrees. So I tried one and three:
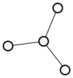
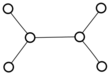
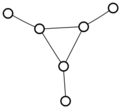
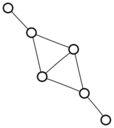
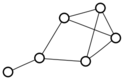
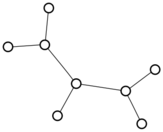
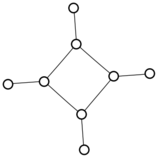
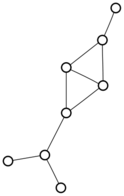
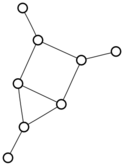
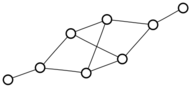
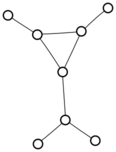
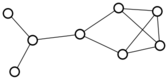
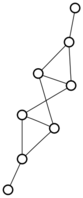
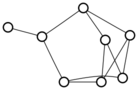
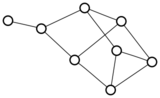
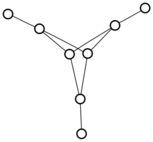
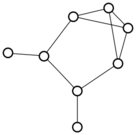
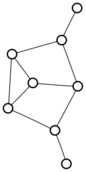
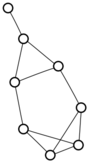
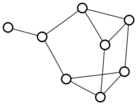
There were only twenty results, so I was able to look through all of them pretty quickly. The first thing I noticed was that the largest ones had only eight vertices, even though the app also searches graphs with nine. That meant that of all the 261080 connected graphs with order nine, none of them had just degrees one and three.
I checked the orders of the other graphs in the set of twenty: there were four that had six vertices, and one that had four. That meant that every example of a graph with degrees one and three had an even number of vertices. Hmmm.
So is that always true? One trivial property of graphs is that the sum of all of the degrees must be even — this is because when you sum the degrees of the vertices, you necessarily count every edge exactly twice. So we’re looking at graphs where all of the degrees are one and three, and we know they have to sum to an even number.
But if you want a set of odd numbers to sum to an even number, you have to have an even number of odd numbers in the set — two odds always sum to an even, so if you have an even number of odd numbers, you can pair them up and get half as many even numbers. But if you have an odd number of odd numbers, one will be left out, and the total sum will have to be odd.
So yadda yum bladdy blah and every graph with degrees one and three must have an even number of vertices. One of my favorite kinds of proofs are the kind that prove something is impossible, despite the fact that you can imagine a whole host of possible scenarios where it might be true. There’s certainly an infinite number of this kind of graph, but no matter which one you choose (or whatever even-ordered graph of any kind that you choose), there is never a way to add just one vertex such that the new graph has only degrees one and three.
Internet Marketing Experts
2010-07-23The other day I received a one-sentence message from the contact page on this site:
We are Internet Marketing experts who can help you answer these questions, drive mass traffic to your site, and dramatically increase sales.
This was a relief, because I had been trying to answer these questions. Also I haven’t had a sale around here for as long as I can remember.
Comments
More Polyominoes
2010-07-22Despite having a pile of ideas and plans, and of course never enough time to implement them, I was able to heave out some planned and requested features for the Polyomino Tiler.
There are a handful of minor UI improvements, and two major new features. The first is the ability to specifically assign colors to certain tiles, as well as expanding the list of provided colors and allowing for arbitrary colors (in hex format) to be added. That and the fact that the heptominoes are now also included enable the following image:

The second new feature is the ability to distinguish between pieces in a one-sided mode, as well as a fixed mode. By “distinguish”, I mean both that you can decide to include or exclude a particular variant, as well as assign variants their own colors (as the following two images illustrate, respectively).

The above image has the ‘T’ tetromino fixed at one orientation, the ‘S’ tetromino as one-sided, and two fixed variants of the ‘L’ triomino. The image below is all one piece, colored differently for each of the eight orientations.

Well good.
Comments
A New Class
2010-06-22Add this to the list of bizarre things you can do in Ruby:
class Object
def new
Class.new
end
end
p Class.new.new.new.new.new.new.new.new.new.new.new
# prints "#<Class:0x401bf9dc>"
Comments
Suggest An Appropriate Title
2010-06-19The other day on a train I was investigating the different ways that numbers can be represented using an “extended binary” when I happened upon an interesting sequence.
Extended binary has the same values for the digits (20, 21, 22, 23…), but instead of allowing only coefficients of 0 and 1, we allow any natural number. So the number 6 can be represented in any of the following ways:
- 1·22 + 1·21
- 1·22 + 2·20
- 3·21
- 2·21 + 2·20
- 1·21 + 4·20
So the number six has five representations. If we count the number of representations for each number, starting with 0, we get the following sequence:
1, 1, 2, 2, 3, 3, 5, 5, 7, 7, 10, 10, 13, 13, 18, 18, 23, 23, 30, 30, 37, 37, 47, 47, 57, 57, …
The first thing I do when analyzing a sequence is to look at the differences between the successive numbers. In this case every number repeats, but if we remove the repeats, like so:
1, 2, 3, 5, 7, 10, 13, 18, 23, 30, 37, 47, 57, …
And then take the difference between each of these numbers, we get:
1, 1, 2, 2, 3, 3, 5, 5, 7, 7, 10, 10, …
Sloane’s has it as A040039, with the subtitle:
First differences of A033485; also A033485 with terms repeated.
Comments