There’s a way to describe prime numbers without mentioning divisibility (or multiplication, division, or any arithmetic at all actually) that I suspect might be easier to digest for people who aren’t the least bit thrilled by number theory.
We just need one preliminary concept. Consider an arrangement of objects into identical rows forming a rectangular grid, like this:

We’ll call it a rectangle as long as all of its sides are at least two objects long. This should all be pretty intuitive.
Note that in the previous example there are 35 objects in total. We could get this by multiplying, but if we’re trying not to use arithmetic, we could also get it by counting. So because we have a rectangle with 35 objects in it, we’ll say that 35 must be a rectangular number. All it means for a number to be rectangular is that if you have that particular number of objects, you can arrange them into a rectangle somehow. Because the rectangles must have sides at least 2, the smallest rectangular number must be 4:

Having now defined ‘rectangular number’ in terms that I optimistically suspect a preschooler could understand, we can get prime numbers with just this:
A prime number is any number greater than one that is not rectangular.
This is a negative definition for sure, but we can make it constructive by turning it into a method for showing a number is prime. This is as simple as checking all possible rectangle-shapes (or row-lengths). For example, to show that 37 is a prime, we look at what happens when we try to make a rectangle with every possible row length:

















There’s always something leftover. So to be prime is to completely escape all attempts at rectangularization. I think it’s fascinating to consider very large primes, for which there would be millions, trillions, or however arbitrarily many plausible row sizes to make a rectangle from, and none of them work.
Maximally Irregular Graphs -- Part 2
2010-06-06My last post where I introduced the idea of maximally irregular graphs ended with a question — can there be two distinct (non-isomorphic) maximally irregular graphs of the same order? I had found this not to be the case up to order 9, but of course we can’t be sure that there aren’t any without a formal proof.
Within minutes of publishing the first post, I started getting ideas of how such a proof might go, but I didn’t have the opportunity and the will to formalize it until just recently.
First a lemma to simplify a bit. For a graph of n nodes containing all degrees from 1 to (n-1), there will always be one duplicate degree, and I didn’t specify in my definition which degree it might be. So the first thing we should note is that, for orders greater than 3, it can’t be of degree (n-1) OR of degree 1. It can’t be of degree (n-1), because that would mean there are two vertices connected to every other vertex, which demands that every vertex have degree at least 2, which precludes the existence of a vertex of degree 1, which we require. The duplicate can’t be of degree 1 either, because then there are two vertices that are only connected to the one vertex of maximal degree, which precludes the existence of a vertex of degree (n-2), which must necessarily be connected to all but one vertex. So for a large enough graph (> 3 vertices, so that 1≠(n-2)), there will be one unique vertex of degree (n-1), and one unique vertex of degree 1.
Having established that, we can outline the proof. The proof will be one of infinite descent, which will create a contradiction when combined with our observation that only one maximally irregular graph exists for each order less than ten. So given two distinct graphs of order n, we will construct two distinct graphs of order (n-2).
So we assume the existence of two non-isomorphic graphs on n vertices, G and H. Then we construct G’ and H’ by taking the induced subgraph that results from removing the vertices of degree 1 and (n-1) from each graph. All we have to show is that G’ and H’ are maximally irregular for order (n-2), and that they cannot be isomorphic.
To show that they are maximally irregular, consider what happens to the remaining vertices when the largest and smallest degree vertices are removed, as in the example order-15 graph below:
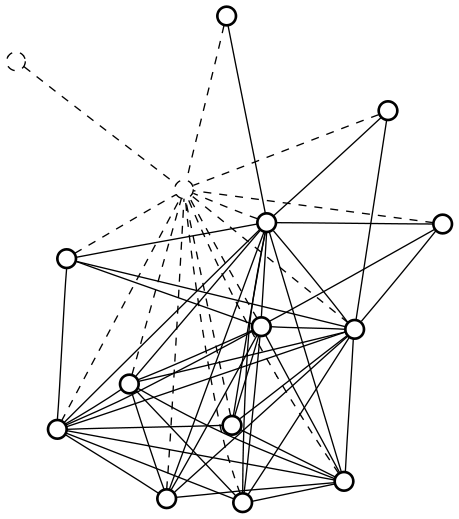
The degree-1 vertex was only connected to the degree-(n-1) vertex, and so its removal does not change the degrees of any of the remaining vertices. The degree-(n-1) vertex, however, was connected to every remaining vertex, and so removing it will decrement the degree of every remaining vertex. So this subset of vertices in the original graph had degrees in the range [2,(n-2)], and so decrementing each of them gives vertices of degrees [1,(n-3)], which is exactly the requirements for a maximally irregular graph of order (n-2).
All that remains is to show that G’ and H’ cannot be isomorphic. We can do this by contradiction — if G’ and H’ are isomorphic, then we can show that G and H must be isomorphic as well, contradicting our original assumption that they are distinct. To show this, let us assume we have a bijection between the vertices of G’ and H’ — I claim that if we use this same bijection for G and H, adding that the vertices of degree (n-1) are mapped to each other and the vertices of degree 1 are mapped to each other, that it will be an isomorphism. This should be obvious once we note that for the degree (n-1) vertices, all other vertices are connected to them, so they are trivially equivalent; and for the degree-1 vertices, they are only connected to the degree (n-1) vertices, which are mapped to each other. So the connections between the two graphs are preserved.
And that’s it. Given any two distinct maximally irregular graphs of the same order, we can produce two smaller distinct maximally irregular graphs by removing two vertices from each graph. This process can be repeated as many times as necessary to produce two distinct maximally irregular graphs of order less than or equal to nine, and we have searched exhaustively to be sure that these do not exist. Therefore, for every order >= 2, there is one unique maximally irregular graph, so we can speak of the maximally irregular graph for any given order.
As a reward for anybody who actually read this far, I supply images of the maximally irregular graphs on 25, 50, 75, and 100 nodes.
Comments
Maximally Irregular Graphs
2010-05-22For no reason in particular, it occurred to me to wonder if there exist any graphs (simple, connected, undirected) that contain vertices of every possible degree (from 1 to (n-1)). A quick mental check should confirm that such a graph would necessarily have exactly two vertices that share the same degree (by the pigeonhole principle). It wasn’t much trouble to set my computer to search my nine-vertices-or-less database, but as I had set it up rather inefficiently, it was taking a few minutes. While I waited, I tried to construct one myself on paper.
I was interested in finding a nine-vertex graph specifically, since that is the largest order in the database. So we start with nine vertices:

For the first step we can connect the graph by choosing vertex A to be the degree-8 vertex. We can also already mark off vertex B as being the degree-1 vertex, so both A and B are complete at this point:
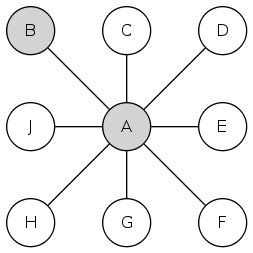
We’ll let C be the degree-2 vertex, and we can accomplish that by connecting it to D:
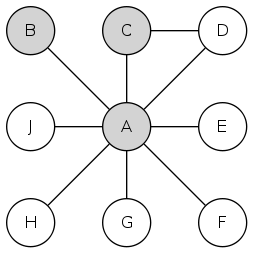
Similarly D will be the degree-3 vertex, and connecting D to E accomplishes this nicely:

Now we need vertex E to have 4 edges, so we connect it with F and G:

Once again, we want five edges for F, so we can accomplish this by connecting it to G, H, and J:

But now it doesn’t look like we can make much more progress. Six of our vertices are already locked up, so the best we can do is to connect all of the remaining three, which won’t suffice since we still need vertices of degree six and seven.

This suggested to me that there must not be any graphs of order 9 with degrees 1-8, and that my computer would search through a couple hundred thousand graphs and come up with nothing. I was surprised, then, when the search returned exactly one result:
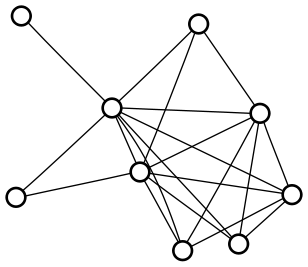
It’s hard to argue with that. So what did I do wrong? After thinking for a minute, I realized it was the choice of connections in the early steps. For example, instead of connecting C to D, I should have connected both C and D to J. Connecting C to D was wasting an edge, in a way. It might be more clear if we redraw the graph in the previous style:

Another way to arrive at this answer would be to work in the other direction — after connecting A to all the other vertices, we then reason that J needs to be connected to 7 vertices and can’t connect to B, so it must necessarily be connected to all the others. Then make similar arguments for H and G, and by that point I think the graph would already be finished.
I also thought it was interesting that there was exactly one graph that fit the requirements. I quickly had the computer search the smaller graphs, and sure enough, for each order, there is only one maximally irregular graph (a term I had to make up, since I don’t have a graph theorist on hand to learn me some vocab):
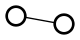
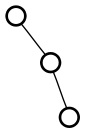
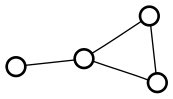
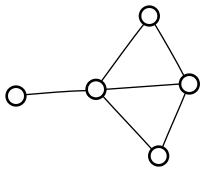
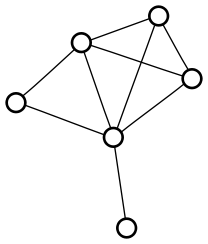
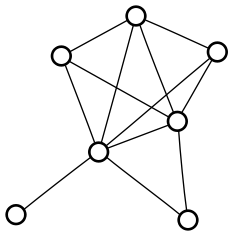
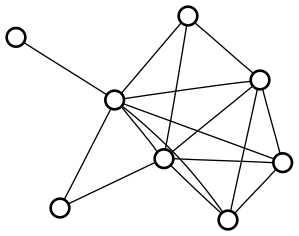
I thought of a pretty simple inductive proof that a maximally irregular graph exists for any order, but I have no idea if there ought to always be exactly one. Isomorphism is extremely easy to check on these graphs, so I’ll start searching for a counterexample.
Comments
MySQL Supported Hack
2010-04-27From the official MySQL documentation comes perhaps the highest combination of software-project-respectability and ugliness-of-officially-recommended-hack that I’ve yet encountered:
To retrieve all rows from a certain offset up to the end of the result set, you can use some large number for the second parameter. This statement retrieves all rows from the 96th row to the last:
SELECT * FROM tbl LIMIT 95,18446744073709551615;
Comments
A Lot of Little Graphs
2010-04-24My recent frolicking about with Graph Theory was facilitated by a database that I populated from these collections, as well as web interface to it with some basic search functions. I just finished polishing the interface to meet my own user-friendliness standards, and have propped it up in the Sandbox here.
It has all of the undirected connected simple graphs with nine vertices or fewer (except the graph with one vertex, which I doubt anyone is interested in), and allows browsing through the database with just about any simple restriction on the attributes of the graph (radius, girth, automorphisms, etc.).
Having the graphs and their attributes pre-computed means that it can be a lot faster to find graphs with particular combinations of characteristics than it would be if everything had to be computed on the fly. It’s also easy to find types of graphs that don’t exist for nine vertices or less, such as asymmetric regular graphs.
As someone with little academic experience with graph theory, I found it a very efficient way to get acquainted with the different types of graph properties and generally increase my familiarity with the subject.
It also tended to prompt deeper questions that aren’t so easy to Google for. For example, I noticed that very few of the graphs had an automorphism-count that was a prime higher than two. Specifically, there are only four of them, all with only three automorphisms, and all on nine vertices. This is one of those:
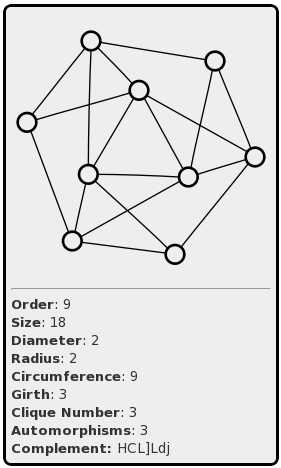
The smallest graph with 2 automorphisms is actually the smallest graph with any edges at all, which is the only connected graph on 2 vertices. So if we form a sequence of the order of the smallest graph with p automorphisms for all primes p, we have the following so far:
2, 9, …
So how does this continue? What is the smallest graph with exactly 5 automorphisms? 7? 11? I can’t find any information on it, but I have to think they might be quite large, such that it would be hard to find them without more sophisticated mathematical analysis. On the hand, they might all be simple variations on the one above.
To avoid the temptation to write a new blog post every time I see an interesting graph, I’ll probably create a list for them. For now, the large-girthed-graphs are fun.
Comments