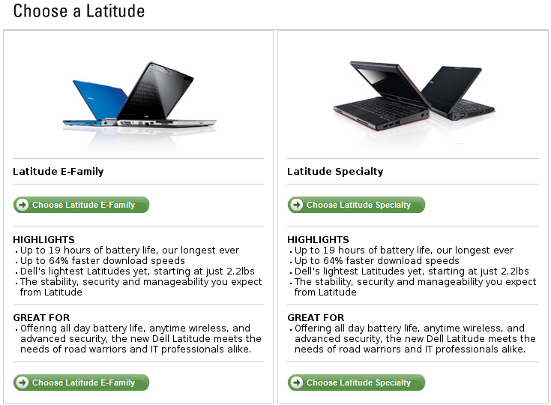
I like Dell’s approach to comparing-and-contrasting their product lines:
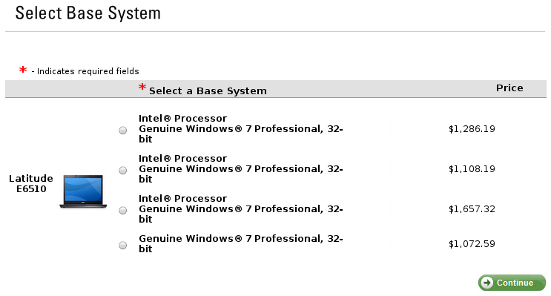
The fun continued when I tried to start customizing things:
Pretty Tiles
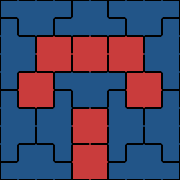
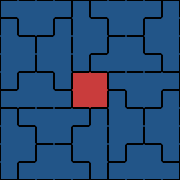
2010-04-02I’m not sure if I should be embarrassed or not, but I think these things are cute:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Comments
Graph Isomorphism is a Problem
2010-04-01I’ve always wanted an excuse to piddle about with graph theory, so when my multi-agent systems class inspired me to think of a naïve attempt at solving the graph-isomorphism problem, I had to try it.
The inspiration was a network routing algorithm where each node in the network keeps a table of the distances to the other nodes through each of its links. I had to wonder if it would be possible to reconstruct the network simply based on one node’s view of the distances. That doesn’t seem very likely, but if we use that information from all of the nodes, I suspect it may even be trivial.
That’s a slightly different question from the graph isomorphism problem though, because a network is labeled, while an unlabeled graph is not. It does, however, suggest a graph invariant that would solve the graph isomorphism problem provided that any two non-isomorphic graphs produce a different invariant.
The invariant is constructed as a three dimensional array by simply listing, for each vertex, the shortest-path distances to the other vertices through each of its edges. The array is then recursively sorted to normalize it. This gives an invariant with seemingly an awful lot of information (at least in my inexperienced opinion). It didn’t seem probable however, that someone with almost no experience in graph theory had solved one of the biggest open problems in graph theory, so I set out to find a counterexample.
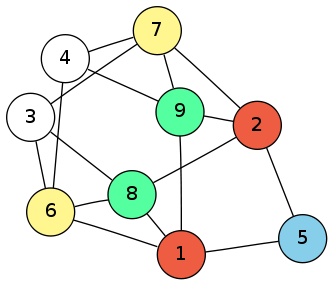
Specifically, I was looking for the smallest pair of non-isomorphic graphs that shared the same invariant. I set one of the computers at my disposal to work on it, and found that the invariant is complete for all graphs with less than nine vertices. For nine-vertex graphs, there are no less than twenty pairs of counterexamples. Here is the pair with the least number of edges:
![HCpdVG] HCpdVG]](/images/blog/58/graph2.png)
The invariant guarantees a few things about these two graphs. They must be the same size and of the same order (same number of edges and vertices), and they must have the same set of edges incident on its vertices: in this case, we can see that both graphs have 6 vertices with 4 edges, 2 vertices with 3 edges, and 1 vertex with 2 edges.
We can tell that the graphs are not isomorphic with a little inspection: if they were isomorphic, then the blue vertices must correspond, since they are the only vertices with two edges. Then the pairs of vertices marked in red must correspond to each other (without knowing which to which), being the two vertices connected to the only vertex with two edges. In both graphs, there are two other vertices that are both connected to the red pair, which are the vertices marked in green. Then there is a third pair of vertices which are connected to one of the red vertices, but not both. These are marked in yellow. Notice that in the first graph, the green and yellow pairs do not share an edge, but in the second graph they do. Therefore, the graphs are not isomorphic.
Showing that they share the same invariant would be a much more laborious task, so I’m going to trust the computer on this one.
This makes me want to start a collection of graph invariants and their corresponding smallest pair of “counterexamples”.
Just because I like pictures of graphs, here’s another one of the twenty pairs I found:
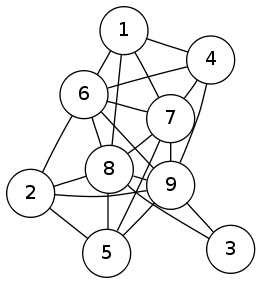
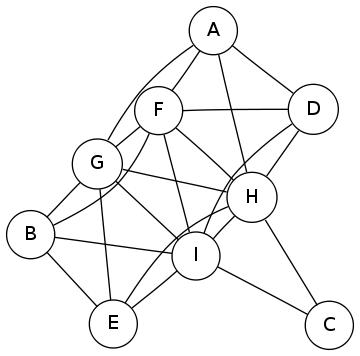
Comments
Polyominoes on Rectangular Grids
2010-03-27Noticing that my Tetris Tiler had been mentioned in a recreational math class at Carnegie Mellon gave me sufficient motivation to dedicate some time during Spring break to pounding out some new features. The most significant is the ability to choose what set of pieces to use, with the set of available pieces being all of the polyominoes of orders two through six. This allows a number of interesting setups that weren’t possible with the fixed set of tetrominos.
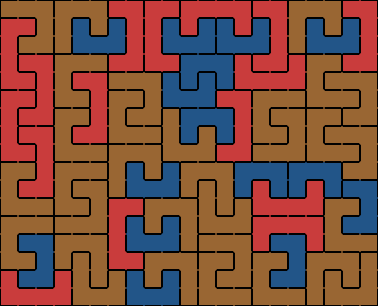
One that I’ve been playing with since I first got the new features functioning is trying to tile an empty grid with a small set of unlikely pieces. Tiling empty grids was never interesting in the older version, because the program always found a boring solution quite quickly and simply. However, with the new features, it’s quite easy to find piece sets that cannot tile a fix-sized rectangular empty grid, and so an interesting problem is finding piece sets for which it’s not at all clear that any such tiling exists. This one is a good example, where each of the pieces are kind of ‘u’ shaped:
This one consists of a bunch of ’t’s:
Another feature I added allows the grid to wrap around vertically or horizontally. This can be used to create seamless repeating patterns, which could be useful, say if you need ideas for tiling your kitchen floor, or a nerdy background for your blog. For a good example, download the image below and set it as your desktop wallpaper, and specify “tiled” (or, if you’re not using Firefox, just click here to see it in a popup window).

It can also be used for this sort of nonsense:
I also added the ability to save grids/tilings, as well as download images (which is where the above images and their links came from). Future features I’m planning on include custom colors, one-sided polyominoes (i.e., distinguishing between mirror images), and an easier-to-use grid editor. You can play with it here.
Comments
Merely Freshmen
2010-03-25I recently noticed that the phrase “we were merely freshmen” from that song by The Verve Pipe has almost entirely ’e’s for vowels (it took me a while to notice the ‘y’, so I originally thought it was exclusive). This suggests a new category of interesting phrases, that only contain one kind of vowel.
We can differentiate between phrases caught in the wild (actually published somehow), and phrases that are reasonable enough that one could imagine them being spoken or written. If we allow for unreasonable phrases (and only require correct syntax), then they could be arbitrarily and trivially long.
I’ll start it off by searching the works of Shakespeare (as found here). In the first scene of The Two Gentlemen of Verona we have the character Speed speaking the line
The shepherd seeks the sheep, and not the sheep the shepherd; but I seek my master, and my master seeks not me; therefore, I am no sheep.
The first phrase is five words long, six if you count the name “Speed” preceding the line. This ought to be beatable. Clearly Shakespeare was only an amateur.

Comments