Considering the strong correlation between my 20-month blog silence and the amount of time I've spent playing with baby toys in the interim, it seems appropriate to start back with a post about those baby toys.
Borromean rings
To start with there are a whole slew of these broken colored rings lying around, presumably intended to be linked together in a chain.
I noticed that the oblong shape allows them to be assembled into Borromean rings.
Top-Heavy Towers
Then there are all of these stereotypical wooden cubes.
It's probably pretty common to probe the limits of top-heavy structures. It occurred to me to try a single block with two blocks atop it, three blocks on the next layer, and so on as high as possible.
Each successive step seemed equally dubious.







After eight layers I ran out of the standard style of blocks and had to fall back on the alternate.

I tried adding an eleventh layer but everything started falling over at that point.
A Googol Hundred
2011-06-08An unsuspecting friend recently reported that her five-year-old son is a fan of big numbers in general, and one number in particular. His favorite number is One Googol and One Hundred (or 10100 + 100), which I will here on out refer to as the number “Samuel” to keep my sentences to a reasonable length. He wanted to be able to count to Samuel in the same way that you might count to other numbers by skipping a regular amount, such as counting to 1000 by tens.
As I started thinking through the various options, I realized that the answer depended on the prime factorization of Samuel, since any number by which you could count to Samuel would have to be a divisor of Samuel. One obvious divisor of Samuel is 100. Counting to Samuel by 100’s is certainly not feasible, but counting to Samuel by “Samuel divided by one hundred”s (or 1098 + 1 or one hundred untrigintillion and one) is, and that was my first suggestion. But then I wondered if the full factorization of Samuel would give other options. Factoring 100-digit numbers isn’t something that I know how to get my computer to do, but fortunately Wolfram Alpha was up to the task.
The result revealed that there are actually quite a handful of options for counting to Samuel in a reasonable amount of time, so I thought I would present them here, just for the joy of looking at really big numbers written out in words. These are all the numbers you can count to Samuel by in fewer than a thousand steps, sorted by and labeled by number of steps:
- 2: five duotrigintillion and fifty
- 4: two duotrigintillion five hundred untrigintillion and twenty-five
- 5: two duotrigintillion and twenty
- 10: one duotrigintillion and ten
- 20: five hundred untrigintillion and five
- 25: four hundred untrigintillion and four
- 29: three hundred and forty-four untrigintillion eight hundred and twenty-seven trigintillion five hundred and eighty-six novemvigintillion two hundred and six octovigintillion eight hundred and ninety-six septemvigintillion five hundred and fifty-one sesvigintillion seven hundred and twenty-four quinquavigintillion one hundred and thirty-seven quattuorvigintillion nine hundred and thirty-one tresvigintillion thirty-four duovigintillion four hundred and eighty-two unvigintillion seven hundred and fifty-eight vigintillion six hundred and twenty novemdecillion six hundred and eighty-nine octodecillion six hundred and fifty-five septendecillion one hundred and seventy-two sexdecillion four hundred and thirteen quindecillion seven hundred and ninety-three quattuordecillion one hundred and three tredecillion four hundred and forty-eight duodecillion two hundred and seventy-five undecillion eight hundred and sixty-two decillion sixty-eight nonillion nine hundred and sixty-five octillion five hundred and seventeen septillion two hundred and forty-one sextillion three hundred and seventy-nine quintillion three hundred and ten quadrillion three hundred and forty-four trillion eight hundred and twenty-seven billion five hundred and eighty-six million two hundred and six thousand nine hundred
- 50: two hundred untrigintillion and two
- 58: one hundred and seventy-two untrigintillion four hundred and thirteen trigintillion seven hundred and ninety-three novemvigintillion one hundred and three octovigintillion four hundred and forty-eight septemvigintillion two hundred and seventy-five sesvigintillion eight hundred and sixty-two quinquavigintillion sixty-eight quattuorvigintillion nine hundred and sixty-five tresvigintillion five hundred and seventeen duovigintillion two hundred and forty-one unvigintillion three hundred and seventy-nine vigintillion three hundred and ten novemdecillion three hundred and forty-four octodecillion eight hundred and twenty-seven septendecillion five hundred and eighty-six sexdecillion two hundred and six quindecillion eight hundred and ninety-six quattuordecillion five hundred and fifty-one tredecillion seven hundred and twenty-four duodecillion one hundred and thirty-seven undecillion nine hundred and thirty-one decillion thirty-four nonillion four hundred and eighty-two octillion seven hundred and fifty-eight septillion six hundred and twenty sextillion six hundred and eighty-nine quintillion six hundred and fifty-five quadrillion one hundred and seventy-two trillion four hundred and thirteen billion seven hundred and ninety-three million one hundred and three thousand four hundred and fifty
- 100: one hundred untrigintillion and one
- 101: ninety-nine untrigintillion nine trigintillion nine hundred novemvigintillion nine hundred and ninety octovigintillion ninety-nine septemvigintillion nine sesvigintillion nine hundred quinquavigintillion nine hundred and ninety quattuorvigintillion ninety-nine tresvigintillion nine duovigintillion nine hundred unvigintillion nine hundred and ninety vigintillion ninety-nine novemdecillion nine octodecillion nine hundred septendecillion nine hundred and ninety sexdecillion ninety-nine quindecillion nine quattuordecillion nine hundred tredecillion nine hundred and ninety duodecillion ninety-nine undecillion nine decillion nine hundred nonillion nine hundred and ninety octillion ninety-nine septillion nine sextillion nine hundred quintillion nine hundred and ninety quadrillion ninety-nine trillion nine billion nine hundred million nine hundred and ninety thousand one hundred
- 116: eighty-six untrigintillion two hundred and six trigintillion eight hundred and ninety-six novemvigintillion five hundred and fifty-one octovigintillion seven hundred and twenty-four septemvigintillion one hundred and thirty-seven sesvigintillion nine hundred and thirty-one quinquavigintillion thirty-four quattuorvigintillion four hundred and eighty-two tresvigintillion seven hundred and fifty-eight duovigintillion six hundred and twenty unvigintillion six hundred and eighty-nine vigintillion six hundred and fifty-five novemdecillion one hundred and seventy-two octodecillion four hundred and thirteen septendecillion seven hundred and ninety-three sexdecillion one hundred and three quindecillion four hundred and forty-eight quattuordecillion two hundred and seventy-five tredecillion eight hundred and sixty-two duodecillion sixty-eight undecillion nine hundred and sixty-five decillion five hundred and seventeen nonillion two hundred and forty-one octillion three hundred and seventy-nine septillion three hundred and ten sextillion three hundred and forty-four quintillion eight hundred and twenty-seven quadrillion five hundred and eighty-six trillion two hundred and six billion eight hundred and ninety-six million five hundred and fifty-one thousand seven hundred and twenty-five
- 145: sixty-eight untrigintillion nine hundred and sixty-five trigintillion five hundred and seventeen novemvigintillion two hundred and forty-one octovigintillion three hundred and seventy-nine septemvigintillion three hundred and ten sesvigintillion three hundred and forty-four quinquavigintillion eight hundred and twenty-seven quattuorvigintillion five hundred and eighty-six tresvigintillion two hundred and six duovigintillion eight hundred and ninety-six unvigintillion five hundred and fifty-one vigintillion seven hundred and twenty-four novemdecillion one hundred and thirty-seven octodecillion nine hundred and thirty-one septendecillion thirty-four sexdecillion four hundred and eighty-two quindecillion seven hundred and fifty-eight quattuordecillion six hundred and twenty tredecillion six hundred and eighty-nine duodecillion six hundred and fifty-five undecillion one hundred and seventy-two decillion four hundred and thirteen nonillion seven hundred and ninety-three octillion one hundred and three septillion four hundred and forty-eight sextillion two hundred and seventy-five quintillion eight hundred and sixty-two quadrillion sixty-eight trillion nine hundred and sixty-five billion five hundred and seventeen million two hundred and forty-one thousand three hundred and eighty
- 202: forty-nine untrigintillion five hundred and four trigintillion nine hundred and fifty novemvigintillion four hundred and ninety-five octovigintillion forty-nine septemvigintillion five hundred and four sesvigintillion nine hundred and fifty quinquavigintillion four hundred and ninety-five quattuorvigintillion forty-nine tresvigintillion five hundred and four duovigintillion nine hundred and fifty unvigintillion four hundred and ninety-five vigintillion forty-nine novemdecillion five hundred and four octodecillion nine hundred and fifty septendecillion four hundred and ninety-five sexdecillion forty-nine quindecillion five hundred and four quattuordecillion nine hundred and fifty tredecillion four hundred and ninety-five duodecillion forty-nine undecillion five hundred and four decillion nine hundred and fifty nonillion four hundred and ninety-five octillion forty-nine septillion five hundred and four sextillion nine hundred and fifty quintillion four hundred and ninety-five quadrillion forty-nine trillion five hundred and four billion nine hundred and fifty million four hundred and ninety-five thousand and fifty
- 281: thirty-five untrigintillion five hundred and eighty-seven trigintillion one hundred and eighty-eight novemvigintillion six hundred and twelve octovigintillion ninety-nine septemvigintillion six hundred and forty-four sesvigintillion one hundred and twenty-eight quinquavigintillion one hundred and thirteen quattuorvigintillion eight hundred and seventy-nine tresvigintillion three duovigintillion five hundred and fifty-eight unvigintillion seven hundred and eighteen vigintillion eight hundred and sixty-one novemdecillion two hundred and nine octodecillion nine hundred and sixty-four septendecillion four hundred and twelve sexdecillion eight hundred and eleven quindecillion three hundred and eighty-seven quattuordecillion nine hundred tredecillion three hundred and fifty-five duodecillion eight hundred and seventy-one undecillion eight hundred and eighty-six decillion one hundred and twenty nonillion nine hundred and ninety-six octillion four hundred and forty-one septillion two hundred and eighty-one sextillion one hundred and thirty-eight quintillion seven hundred and ninety quadrillion thirty-five trillion five hundred and eighty-seven billion one hundred and eighty-eight million six hundred and twelve thousand and one hundred
- 290: thirty-four untrigintillion four hundred and eighty-two trigintillion seven hundred and fifty-eight novemvigintillion six hundred and twenty octovigintillion six hundred and eighty-nine septemvigintillion six hundred and fifty-five sesvigintillion one hundred and seventy-two quinquavigintillion four hundred and thirteen quattuorvigintillion seven hundred and ninety-three tresvigintillion one hundred and three duovigintillion four hundred and forty-eight unvigintillion two hundred and seventy-five vigintillion eight hundred and sixty-two novemdecillion sixty-eight octodecillion nine hundred and sixty-five septendecillion five hundred and seventeen sexdecillion two hundred and forty-one quindecillion three hundred and seventy-nine quattuordecillion three hundred and ten tredecillion three hundred and forty-four duodecillion eight hundred and twenty-seven undecillion five hundred and eighty-six decillion two hundred and six nonillion eight hundred and ninety-six octillion five hundred and fifty-one septillion seven hundred and twenty-four sextillion one hundred and thirty-seven quintillion nine hundred and thirty-one quadrillion thirty-four trillion four hundred and eighty-two billion seven hundred and fifty-eight million six hundred and twenty thousand six hundred and ninety
- 404: twenty-four untrigintillion seven hundred and fifty-two trigintillion four hundred and seventy-five novemvigintillion two hundred and forty-seven octovigintillion five hundred and twenty-four septemvigintillion seven hundred and fifty-two sesvigintillion four hundred and seventy-five quinquavigintillion two hundred and forty-seven quattuorvigintillion five hundred and twenty-four tresvigintillion seven hundred and fifty-two duovigintillion four hundred and seventy-five unvigintillion two hundred and forty-seven vigintillion five hundred and twenty-four novemdecillion seven hundred and fifty-two octodecillion four hundred and seventy-five septendecillion two hundred and forty-seven sexdecillion five hundred and twenty-four quindecillion seven hundred and fifty-two quattuordecillion four hundred and seventy-five tredecillion two hundred and forty-seven duodecillion five hundred and twenty-four undecillion seven hundred and fifty-two decillion four hundred and seventy-five nonillion two hundred and forty-seven octillion five hundred and twenty-four septillion seven hundred and fifty-two sextillion four hundred and seventy-five quintillion two hundred and forty-seven quadrillion five hundred and twenty-four trillion seven hundred and fifty-two billion four hundred and seventy-five million two hundred and forty-seven thousand five hundred and twenty-five
- 505: nineteen untrigintillion eight hundred and one trigintillion nine hundred and eighty novemvigintillion one hundred and ninety-eight octovigintillion nineteen septemvigintillion eight hundred and one sesvigintillion nine hundred and eighty quinquavigintillion one hundred and ninety-eight quattuorvigintillion nineteen tresvigintillion eight hundred and one duovigintillion nine hundred and eighty unvigintillion one hundred and ninety-eight vigintillion nineteen novemdecillion eight hundred and one octodecillion nine hundred and eighty septendecillion one hundred and ninety-eight sexdecillion nineteen quindecillion eight hundred and one quattuordecillion nine hundred and eighty tredecillion one hundred and ninety-eight duodecillion nineteen undecillion eight hundred and one decillion nine hundred and eighty nonillion one hundred and ninety-eight octillion nineteen septillion eight hundred and one sextillion nine hundred and eighty quintillion one hundred and ninety-eight quadrillion nineteen trillion eight hundred and one billion nine hundred and eighty million one hundred and ninety-eight thousand and twenty
- 562: seventeen untrigintillion seven hundred and ninety-three trigintillion five hundred and ninety-four novemvigintillion three hundred and six octovigintillion forty-nine septemvigintillion eight hundred and twenty-two sesvigintillion sixty-four quinquavigintillion fifty-six quattuorvigintillion nine hundred and thirty-nine tresvigintillion five hundred and one duovigintillion seven hundred and seventy-nine unvigintillion three hundred and fifty-nine vigintillion four hundred and thirty novemdecillion six hundred and four octodecillion nine hundred and eighty-two septendecillion two hundred and six sexdecillion four hundred and five quindecillion six hundred and ninety-three quattuordecillion nine hundred and fifty tredecillion one hundred and seventy-seven duodecillion nine hundred and thirty-five undecillion nine hundred and forty-three decillion sixty nonillion four hundred and ninety-eight octillion two hundred and twenty septillion six hundred and forty sextillion five hundred and sixty-nine quintillion three hundred and ninety-five quadrillion seventeen trillion seven hundred and ninety-three billion five hundred and ninety-four million three hundred and six thousand and fifty
- 580: seventeen untrigintillion two hundred and forty-one trigintillion three hundred and seventy-nine novemvigintillion three hundred and ten octovigintillion three hundred and forty-four septemvigintillion eight hundred and twenty-seven sesvigintillion five hundred and eighty-six quinquavigintillion two hundred and six quattuorvigintillion eight hundred and ninety-six tresvigintillion five hundred and fifty-one duovigintillion seven hundred and twenty-four unvigintillion one hundred and thirty-seven vigintillion nine hundred and thirty-one novemdecillion thirty-four octodecillion four hundred and eighty-two septendecillion seven hundred and fifty-eight sexdecillion six hundred and twenty quindecillion six hundred and eighty-nine quattuordecillion six hundred and fifty-five tredecillion one hundred and seventy-two duodecillion four hundred and thirteen undecillion seven hundred and ninety-three decillion one hundred and three nonillion four hundred and forty-eight octillion two hundred and seventy-five septillion eight hundred and sixty-two sextillion sixty-eight quintillion nine hundred and sixty-five quadrillion five hundred and seventeen trillion two hundred and forty-one billion three hundred and seventy-nine million three hundred and ten thousand three hundred and forty-five
- 725: thirteen untrigintillion seven hundred and ninety-three trigintillion one hundred and three novemvigintillion four hundred and forty-eight octovigintillion two hundred and seventy-five septemvigintillion eight hundred and sixty-two sesvigintillion sixty-eight quinquavigintillion nine hundred and sixty-five quattuorvigintillion five hundred and seventeen tresvigintillion two hundred and forty-one duovigintillion three hundred and seventy-nine unvigintillion three hundred and ten vigintillion three hundred and forty-four novemdecillion eight hundred and twenty-seven octodecillion five hundred and eighty-six septendecillion two hundred and six sexdecillion eight hundred and ninety-six quindecillion five hundred and fifty-one quattuordecillion seven hundred and twenty-four tredecillion one hundred and thirty-seven duodecillion nine hundred and thirty-one undecillion thirty-four decillion four hundred and eighty-two nonillion seven hundred and fifty-eight octillion six hundred and twenty septillion six hundred and eighty-nine sextillion six hundred and fifty-five quintillion one hundred and seventy-two quadrillion four hundred and thirteen trillion seven hundred and ninety-three billion one hundred and three million four hundred and forty-eight thousand two hundred and seventy-six
Comments
The Ham Sandwich Theorem
2011-06-07Once again Algebraic Topology compelled me to write code. This time it was the Ham Sandwich Theorem, when I realized that it wouldn’t be too hard to demonstrate the two dimensional version of the theorem with another interactive doohickey.
The interpretation from which the Ham Sandwich Theorem gets its name says that if you have two slices of bread and a slice of ham between them, then no matter what their respective shapes or volumes or how they are positioned relative to each other, it’s always possible to make a single straight slice through the sandwich resulting in all three pieces being exactly bisected.
The Ham Sandwich Theorem applies to any N solids in N-dimensional space, so the 2D version says that any two sets of geometric shapes can be simultaneously bisected by a line. I said “two sets” rather than “two shapes” because the theorem actually doesn’t rely on the shapes even being connected. So we can talk about a collection of red and blue circles, as in the image below:
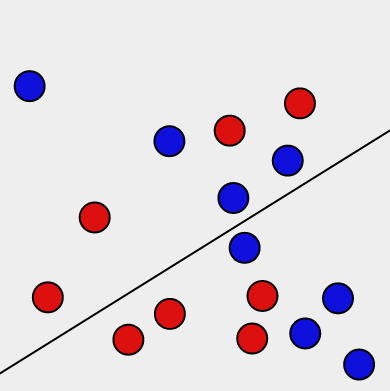
No matter how the circles are arranged, and no matter how many of them there are, there will always be at least one line that bisects both sets by area simultaneously. The interactive version lets you add, remove, and rearrange the circles.
Comments
Primitive Triangles
2011-05-28I’ve been spending some of my free time the last week and a half watching Norman Wildberger’s Lectures on Algebraic Topology. One of the things I’ve learned is that an m-by-n rectangle with integer dimensions can be partitioned into 2×m×n triangles with area ½ and corners at integral points. This fact by itself is rather obvious, given the most regular partitioning shown below:
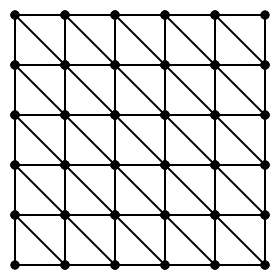
The part that surprised me is that the sides of the triangles can be arbitrarily long, allowing a variety of different shapes, and the whole thing still works out. Here’s another way to partition the 5-by-5 rectangle:
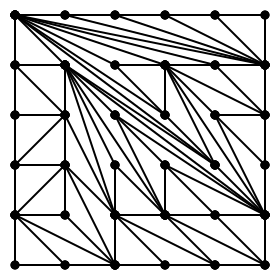
The fact that they all have the same area is a consequence of Pick’s Theorem. I wanted to see what sorts of partitionings you get by starting with a bare rectangle and adding lines at random. And that’s exactly where the image above came from.
Here are a couple more, just for fun.
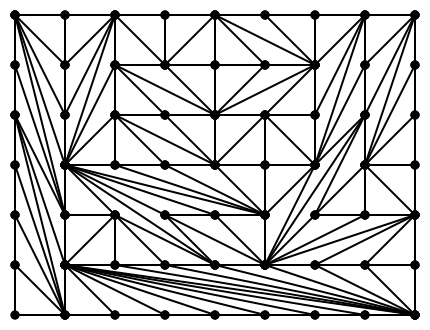
Comments
These Two Graphs Do This
2011-05-17I’ve been doing some academic research lately that involves computing the probability that a network that grows by adding links in a particular way will end up with certain properties. I went about this by generating all graphs up to a particular order, and so I used unlabeled graphs, which seemed good enough and meant I had far fewer graphs to deal with.
Eventually I decided that it would be more realistic to at least pretend that the computation was being done on labeled graphs (by making sure that I got the same answer either way). This led me to a discovery that wasn’t too surprising by itself, but I was surprised that I hadn’t thought of it earlier: there are (unlabeled) graphs for which adding two completely different edges will produce the same graph. For illustration I found the smallest example:
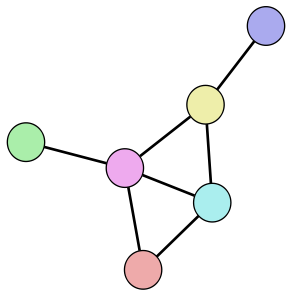
The first thing to notice about this graph is that it’s completely asymmetric: The pink and orange vertices have the distinction of being the only degree-4 and degree-2 vertices respectively. The blue vertex is distinguished as being the only vertex adjacent to both the pink and orange. The green vertex is the only degree-1 vertex adjacent to the pink, and the yellow and blue vertices are clearly distinct from each other as they have different degrees. So there is no symmetry in this graph whatsoever, which means that any edge we could conceivably add to it would be “different” from any other edge we could add.
So there are two different edges we can add to this graph and end up with graphs that are isomorphic to each other. Specifically, by adding either edge we will end up with this graph:
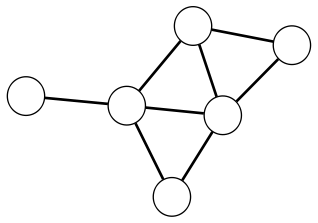
Another way to say it is that our original colored graph is a subgraph of this graph in two different ways. This can be easily illustrated by repositioning the vertices so they match the supergraph in two different ways:
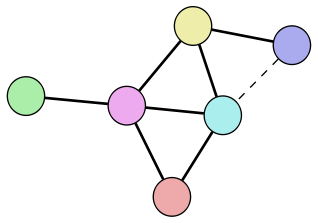
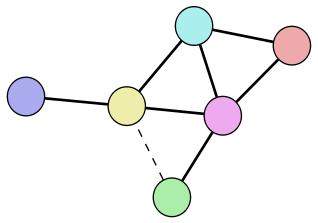
You should be able to confirm visually that these two are the same as the original graph, and that they can each be transformed into the supergraph by adding a single edge, which is drawn dashed.
So this is the smallest pair of graphs that has this property, and in fact the only example on six vertices. I’m not sure how common they are. It is not a straightforward thing to google.
Another cool thing is that, apparently just by coincidence, the smaller graph and the larger graph are complements of each other. So if we take the original graph and reverse all the links like so:
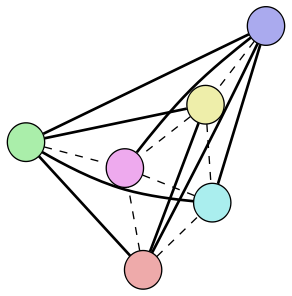
we end up with the same graph that we got by adding an edge:
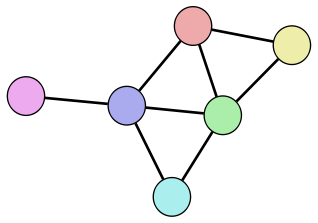
Kinda weird.







Comments