UPDATE: Thanks to David MacIver for pointing out that the problem being reduced to here is the Exact Cover problem, and the reduction was described by Donald Knuth in his Dancing Links paper.
Over eight years ago I created the Polyomino Tiler (a browser application that attempts to tile arbitrary grids with sets of polyominoes), but I haven't ever written about the algorithm it uses.
If any aspects of what follows are confusing, it may help to play with the polyomino tiler a bit to get a better idea for what it's doing.
There are a couple aspects of the problem that combine to make it challenging:
- the set of available polyominos is fully customizable up to the heptominoes; each polyomino can be restricted to specific flips/rotations
- the grid can be any subset of a rectangular grid (or a cylinder/torus)
So the algorithm needs to be generic enough to not get bogged down in all the edge cases resulting from these two facts.
The two key components of the algorithm are:
- abstract away the geometric details by constructing a graph that describes all the possibilities
- apply certain heuristics to a generic backtracking search algorithm on that graph
Placements
The main preprocessing step is to calculate all possible placements of all available pieces. When hundreds of piece variants are available this step can be lengthy, and the result can require a lot of memory. But the result is essentially a bipartite graph (or, in database terms, a many-to-many relationship) between placements and grid points.
For example, given this 2x3 grid:
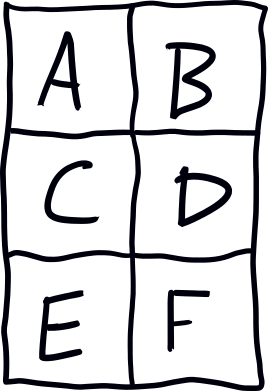
and restricting ourselves to the L-shaped trominoes to keep the visuals tractable, the placement graph looks like this:

Notice that all of the geometric details have been abstracted away; this means that the rest of the algorithm could just as easily be applied to grids of triangles, or hexagons, or hyperbolic grids, or higher dimensions.
Search
Given the bipartite graph, the problem of tiling the grid can be reformulated as the problem of finding a subset of the placements that, as a whole, is connected to every one of the grid points exactly one time.
The search algorithm is a backtracking algorithm that at each step chooses an untiled grid point and a random placement associated with that grid point; it adds that placement to the solution set and then tries to tile the remainder of the grid (taking note of which placements are invalidated by the one selected). If it fails to tile the rest of the grid, then it tries the next placement. If it runs out of placements, then the grid must be untileable.
For example, if we decide to start tiling the above grid from grid point A, the search tree might look like this:
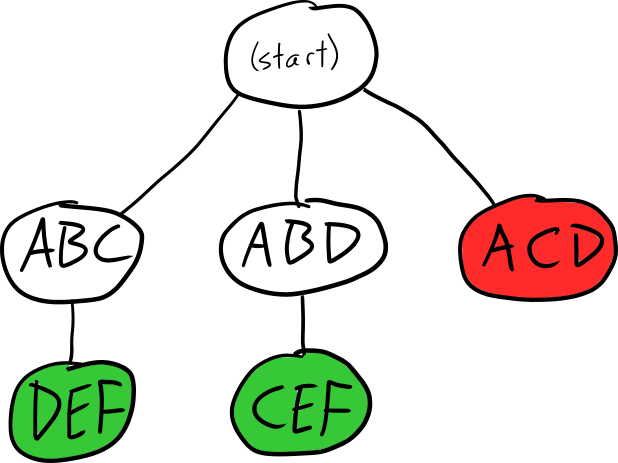
Depending on the order that we search the children, we could either end up with the ABC-DEF tiling or the ABD-CEF tiling; if we visit the ACD branch first, we'll have to backtrack since there's no solution in that direction.
The reason the tree is so sparse is that each time we descend we remove placements from the graph that conflict with the one chosen. E.g., when we descend to ABC, the graph is updated to look like this:
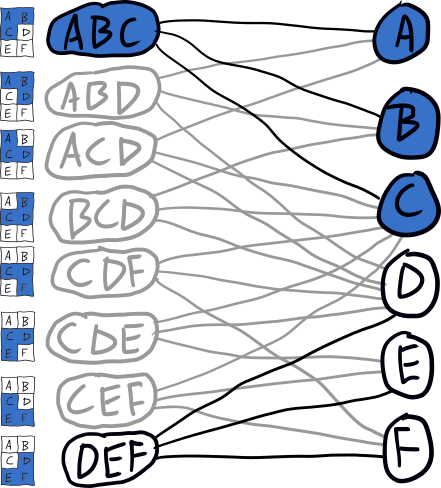
This basic search algorithm is specialized with several heuristics/optimizations.
Untileability from Zero Placements
Since every placement we select makes several other placements impossible, it's easy to get to a point where there is some grid point that no longer has any possible placements. This is the most common sign of untileability, and it means we need to backtrack and try something different.
For example, if we descended down the ACD branch of the search tree, the graph would look like this, and the existence of grid points with no placements indicates that there's no solution.
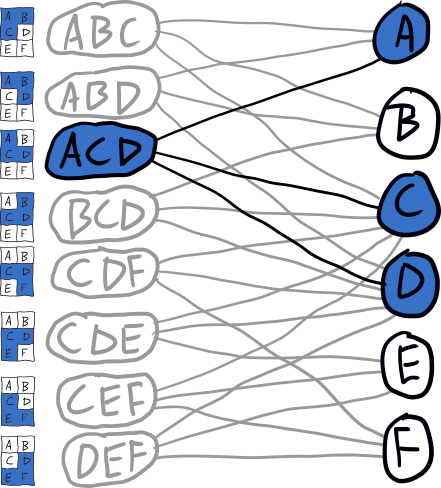
Untileability with Number Theory
A given set of polyominoes places restrictions on what grids can be tiled purely based on their size. This is solely a function of the set of distinct sizes of the polyominoes.
For example, with the tetrominoes, only grids whose size is a multiple of four can be tiled. If the polyominoes have sizes 4 and 6, then only grids whose size is an even number greater than two can be tiled. This kind of analysis is closely related to the coin problem.
Further, if a grid consists of disconnected subcomponents, then we can analyze the tileability of each one separately, and conclude that the whole grid can't be tileable if any of the subcomponents is not tileable.
For example, this grid has been disconnected, and even though the size of both pieces together is a multiple of three and so could theoretically be tiled by trominoes, the individual subcomponents do not have a multiple of three grid points, and so neither of them are tileable.

Smallest Subcomponents First
If the grid at any point becomes disconnected, we immediately restrict the algorithm to the smallest subcomponent and try to tile that completely before moving on to the next one. The logic here is that if the disconnected grid as a whole can't be tiled, there's a decent chance that the smallest subcomponent can't be tiled. The smallest subcomponent is also likely the one that we can finish searching the fastest, and so this hopefully leads to a more aggressive pruning of the search space.
For example, this grid has a small component and a large component, and the small component can't be tiled with trominoes (can you figure out why?); tiling the smaller one first means we find out about this problem quickly, rather than waiting until the whole large subcomponent has been tiled.

Tile the most restricted grid points first
Within a subcomponent, we select the next grid point to tile based on the number of remaining placements it has. It is not uncommon for there to be a grid tile with only a single option, and in those cases it's important to place that piece immediately, since it likely decreases the size of the search space by eliminating other placements (and potentially causing more grid points to have only one option).
When there's not a grid point with a single placement, we still prioritize grid points with the fewest number of placements, since these are intuitively the most "difficult" parts of the grid to tile, which makes them more likely to be rendered untileable by other placements.
For example, in this grid the untiled grid point in the bottom left corner has only one possible placement with trominoes; tiling it lets us eliminate seven other placements that conflict with the forced placement.

Split the grid whenever possible
The last heuristic is a little crude but still useful. The motivation is that being able to split the grid into subcomponents is useful (since they can be analyzed independently), and so if we have the opportunity to split it by placing a piece, we should do so. So the precise rule is that, when there aren't any single-placement grid points (which are higher priority), and there is a single grid point that splits the grid (in graph theory terms, a vertex whose removal disconnects the graph), then we search placements for that grid point next.
For example, there are a couple grid points that disconnect the bottom right portion of this grid from the rest of it; either of these could be chosen for the next search step.

This approach could probably be generalized to something that tends to select grid points that make the grid easier to split, rather than only acting on this principle when it can be achieved in a single step. However, this would likely be somewhat in tension with the prioritization of the most restricted grid points, so I'm not sure how it would work out.
Getting Stuck
Since the polyomino tiling problem is NP-complete, it's not surprising that there's a variety of scenarios where the algorithm gets stuck. Some of these are artifacts of the particular algorithm, and it could conceivably be tweaked to handle those special cases. But I think the algorithm as it is is a decent balance of broad efficacy and simplicity.
The randomness in the algorithm (the ordering of placements for a particular grid point, and to a limited extent the prioritization of grid points) means that sometimes more progress can be made simply by restarting the search.
Possibilities
There are a variety of directions the algorithm could be tweaked; I mentioned one earlier about working more aggressively to split the grid.
Another idea is to optimize the order that placements for a particular grid point are tried. Perhaps placements could be prioritized based on the number of options available for the other grid points involved.
Summary
So to tile an arbitrary grid with an arbitrary set of polyominoes, we:
- calculate all possible placements to obtain a bipartite graph between grid points and placements
- use a backtracking algorithm to search for a subset of placements that exactly tiles the grid
- optimize the algorithm by using various heuristics to prioritize its choices
In hindsight, I believe the initial step of transforming to a graph could be retargeted to transforming to an instance of the SAT problem, in which case a generic SAT solver could be used for the rest of the algorithm. It would be interesting to learn which of the heuristics in my algorithm have analogs in general SAT solvers, and which are particular to tiling problems.
Comments